Al analizar una serie de datos, a veces nos encontramos con valores que no parecen formar parte de la distribución normal de los datos. Estos puntos se conocen como valores atípicos y, como es habitual, no siempre debes confiar en tu intuición para poder detectar si un valor es un valor atípico o no. Existen pruebas que pueden ponerlos de manifiesto y software estadístico como Ellistat para ayudarte con los cálculos.
Desde un punto de vista estadístico, un valor atípico es un valor que no pertenece a la distribución normal de los datos. Puede proceder de :
- Un error de medición o de copia (olvido del punto decimal)
- Una causa especial, como que una pieza no se haya lavado antes de medirla.
Todos los cálculos estadísticos que utilizan las propiedades de la distribución normal (pruebas estadísticas, cálculos de capacidad, cálculos % fuera de tolerancia) son muy sensibles a la presencia de valores atípicos, por lo que es importante comprender su origen y eliminarlos antes de utilizar estos cálculos. También pueden utilizarse pruebas estadísticas no paramétricas, mucho menos sensibles a los valores atípicos.
Se utilizan dos pruebas principales:
- Prueba de Dixon muy interesante cuando el número de datos es bajo (<30)
- Prueba Grubbs puede utilizarse en todos los casos.
Prueba de Dixon
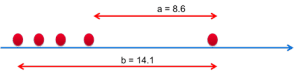
Para utilizar la prueba de Dixon, calcule el cociente :
- b = Alcance global de las mediciones (aquí 14.1)
- a = Distancia entre la pieza sospechosa de ser un valor atípico y su vecino más próximo (aquí 8,6).
La proporción se calcula en %.
A continuación, se compara este informe con la tabla de Dixon:
| Número de piezas | 3 | 5 | 10 | 16 | 20 | 30 |
| Coeficiente máximo | 0.94 | 0.72 | 0.46 | 0.38 | 0.34 | 0.30 |
Si el valor es inferior a la relación máxima sugerida por la tabla, entonces el valor no es un valor atípico. En este caso, la proporción de 62% para 5 piezas es inferior a 72%. Por lo tanto, no se trata de un valor atípico.
Prueba Grubb
Para utilizar la prueba de Grubb, primero calculamos :
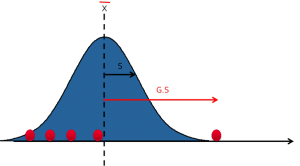
- X: La media de todas las mediciones
- S: Desviación típica de todas las mediciones
- G: Distancia entre el valor sospechoso de ser un valor atípico y la media G.
G=\frac{(Valor - X)}{S}
A continuación, el valor de G obtenido se compara con un límite G :
G_{limite}=\frac{N-1}{\sqrt{N}}.\sqrt{\frac{t^2_{\frac{a}{N},N-2}{}}{N-2 +t^2{}_{\frac{a}{n}}{,} N-2}}
Si el límite es G>G, el valor se considera atípico y viceversa.


