Outlier testing

When analyzing a series of data, we sometimes find ourselves confronted with values that do not appear to be part of the normal distribution of the data. These points are known as outliers and, as usual, you can't always rely on your intuition to detect whether a value is an outlier or not. There are tests that can highlight them and statistical software such as Ellistat to help you with the calculations.

From a statistical point of view, an outlier is a value that does not belong to the normal distribution of the data. It can arise from :

• A measurement or copying error (forgetting the decimal point)
• A special cause, such as a piece not washed before measuring.

All statistical calculations using the properties of the normal law (statistical tests, capability calculations, out-of-tolerance % calculations) are very sensitive to the presence of outliers, so it's important to understand their origin and eliminate them before using these calculations. Non-parametric statistical tests may also be used, as they are much less sensitive to outliers.

Two main tests are used:

• Dixon test very interesting when the number of data is low (<30)
• Grubbs test can be used in all cases.

Dixon test

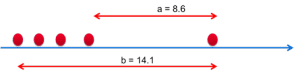
To use the Dixon test, calculate the ratio :

• b = Overall measurement range (here 14.1)
• a = The distance between the part suspected of being an outlier and its nearest neighbor (here 8.6)

The ratio is calculated in %.

This report is then compared with Dixon's table:

If the value is less than the maximum ratio suggested by the table, then the value is not an outlier. Here, the ratio of 62% for 5 pieces is less than 72%. The point is therefore not an outlier.

Grubb test

To use the Grubb test, we first calculate :

• X: Average of all measurements
• S: Standard deviation of all measurements
• G: Distance between the value suspected of being an outlier and the mean G.

G=\frac{(Value - X)}{S}

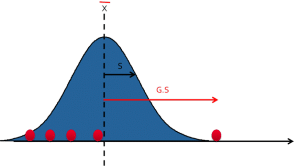
The G value obtained is then compared to a limit G :

G_{limite}=\frac{N-1}{\sqrt{N}}.\sqrt{\frac{t^2_{\frac{a}{N},N-2}{}}{N-2 +t^2{}_{\frac{a}{n}}{,} N-2}}

If G>G limit, the value is considered an outlier, and vice versa.