La distribución de Weibull es la más utilizada para modelizar datos de fiabilidad. El módulo de análisis de datos Ellistat le permite realizar estos análisis con facilidad.
Definiciones: Fiabilidad, Ley de Weibull, Fallo
Fiabilidad:
La fiabilidad es la capacidad de una entidad para realizar una función requerida, en unas condiciones dadas, durante un intervalo de tiempo determinado.
Fracaso:
Un fallo es el fin de la capacidad de un dispositivo para realizar una función esperada. Puede ser parcial (deterioro del rendimiento) o total (fin de la función).
R(t)Probabilidad de que una entidad E no tenga fallos durante el periodo [0; t ], suponiendo que no tiene fallos en el momento t = 0.
F(t)F(t) es la función acumulativa de fallos è F(t) = 1 - R(t)
Densidad de probabilidad f(t) es la tasa de fallos del producto, es decir, la probabilidad de que un producto falle en el intervalo de tiempo [t,t+dt].
λ(t) o tasa de fracaso : λ(t) representa la tasa de fallos de un producto, es decir, la probabilidad de que un producto falle en el intervalo de tiempo [t,t+dt] sabiendo que no falló en el momento t.
- λ(t) disminuye La tasa de defectos disminuye con el tiempo, lo que suele corresponder a defectos precoces. Los productos con defectos intrínsecos se deterioran rápidamente, mientras que los demás duran mucho más.
- λ(t) constante El porcentaje de fallos no depende del tiempo. Existe el mismo riesgo de que un producto falle en un momento t, sea cual sea su vida útil. Se trata de fallos intrínsecos. Es el tipo de fallo que suele darse en los productos electrónicos.
- λ(t) aumenta El índice de fallos aumenta con el tiempo. Existe un riesgo creciente de que un producto falle a medida que aumenta su vida útil. Es el final de la vida útil del producto.
MTTF (tiempo medio hasta el fallo)
El MTTF, más utilizado en la fiabilidad de los productos, es el tiempo medio hasta el primer fallo.
MTBF (tiempo medio entre fallos)
El MTBF (tiempo medio entre fallos) es la media de los intervalos de tiempo entre dos fallos.
Ley de Weibull
Para modelizar la ley de fallos de un producto, es necesario poder modelizar varios tipos de fallos:
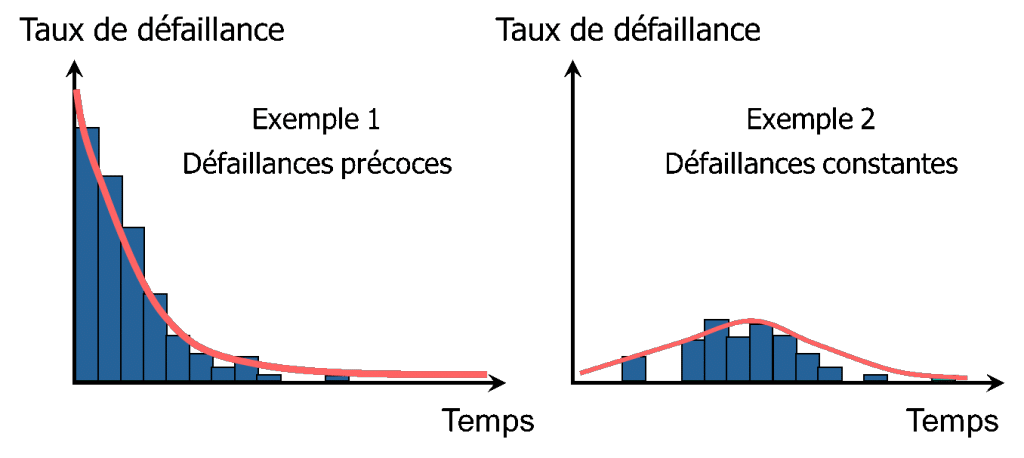
Por este motivo, la ley de Weibull es la más utilizada, ya que permite una gran variabilidad en la forma.
Gracias a su gran flexibilidad, la ley de Weibull puede utilizarse para modelizar el comportamiento de muchos tipos de fallos, como :
- La resistencia a la rotura de los componentes o el esfuerzo necesario para fatigar los metales.
- El tiempo de fallo de un componente electrónico
- Tiempo de avería de los artículos utilizados al aire libre, como los neumáticos de los coches.
- Sistemas que fallan cuando falla el componente más débil del sistema
La ley de Weibull también puede utilizarse para modelizar el comportamiento de diferentes situaciones de vida útil de un mismo componente.
La función de distribución de Weibull es la siguiente :
R\left( t \right)=e-\left( \frac{t-\delta}{\phi} \right)^{\beta}
Tiene 3 parámetros:
- \betaparámetro de forma
- θ: parámetro de escala
- \deltaparámetro de retardo
βparámetro de forma
Permite adaptar la forma de la ley para que se aproxime lo más posible a la tasa de fallos observada:
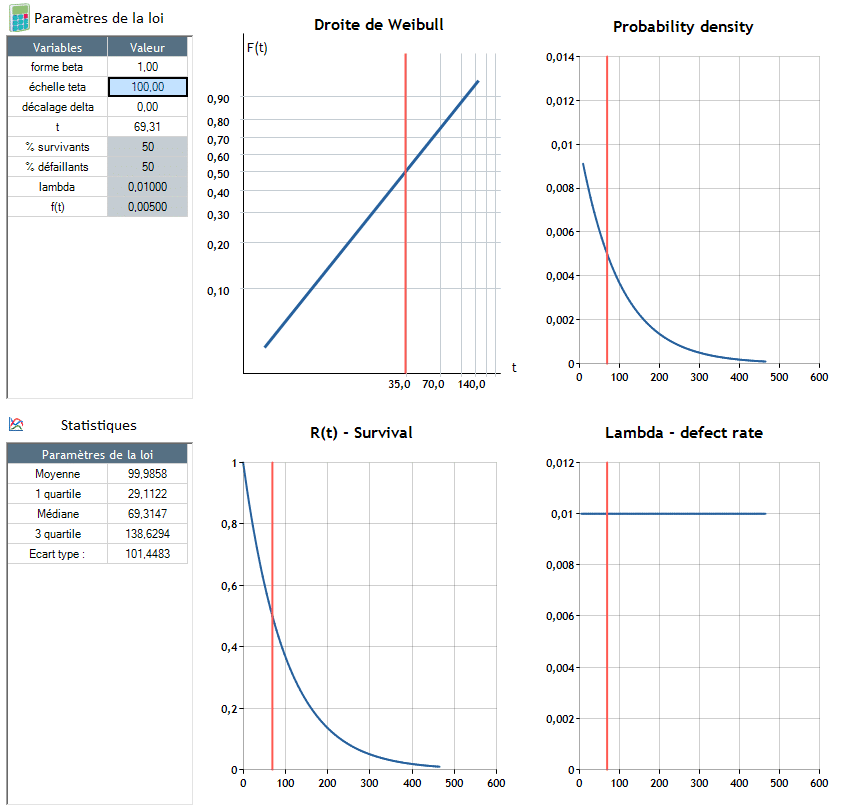
β=1: El porcentaje de fallos es constante (λ constante)
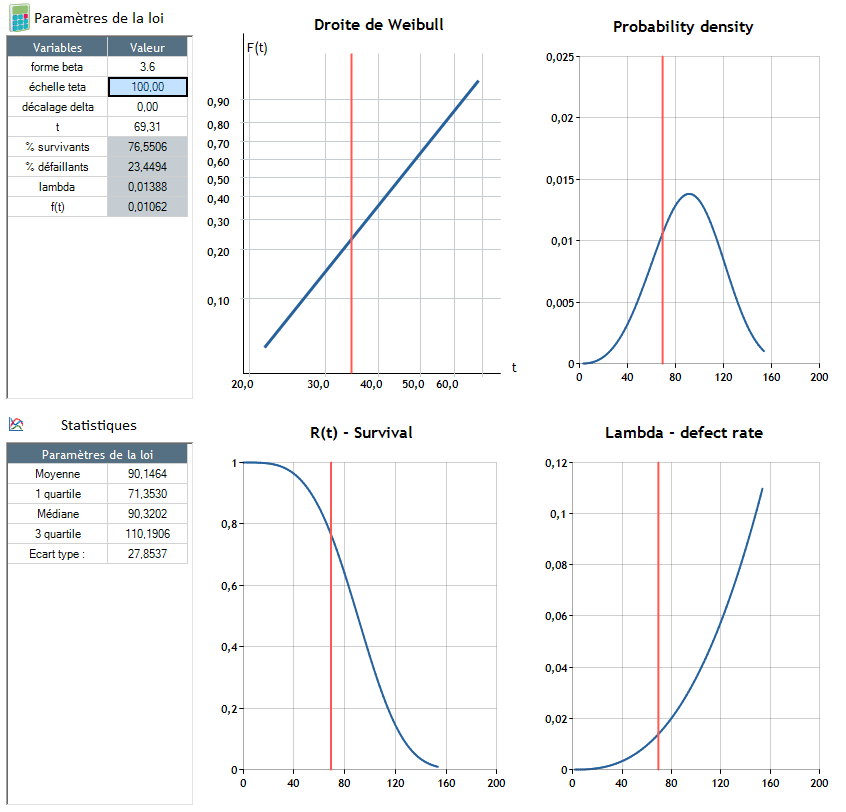
β>1: El porcentaje de fallos aumenta con el tiempo (λ aumentos - final de la vida útil del producto)
θ: parámetro de escala
El parámetro θ se utiliza para ajustar la escala de la ley de distribución a la escala del problema observado, por ejemplo :
El fallo se produce alrededor de t = 90,4
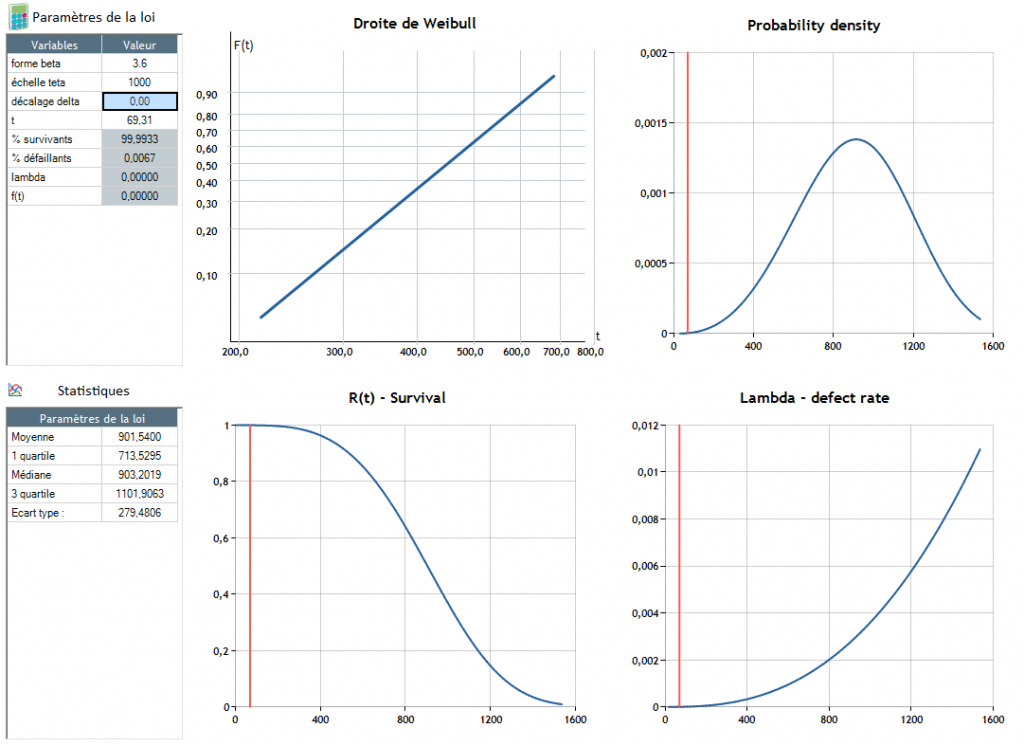
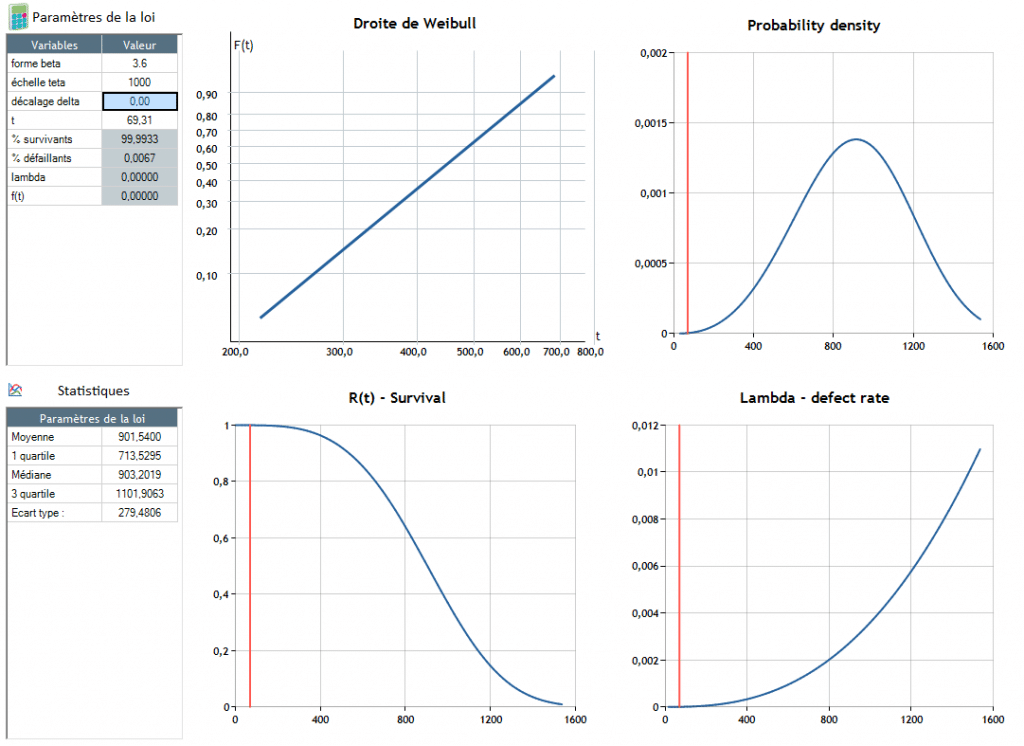
El fallo se produce alrededor de t = 904
δparámetro de retardo
La ley de distribución puede desplazarse mediante un parámetro δ
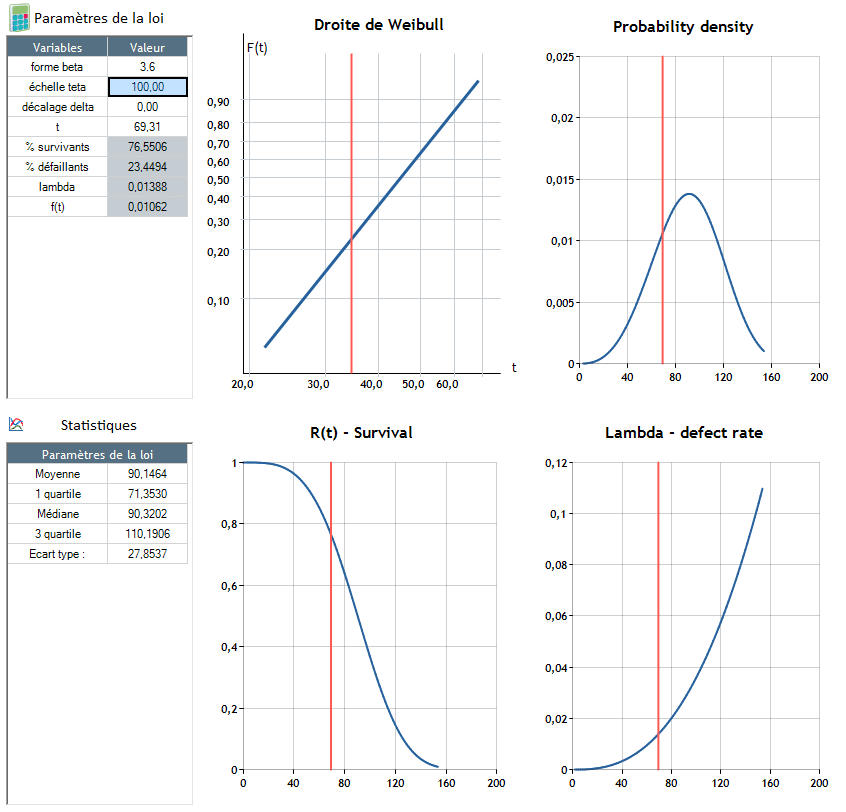
Β = 3,6 - θ = 100, δ = 0
El fallo se produce alrededor de t = 90,4
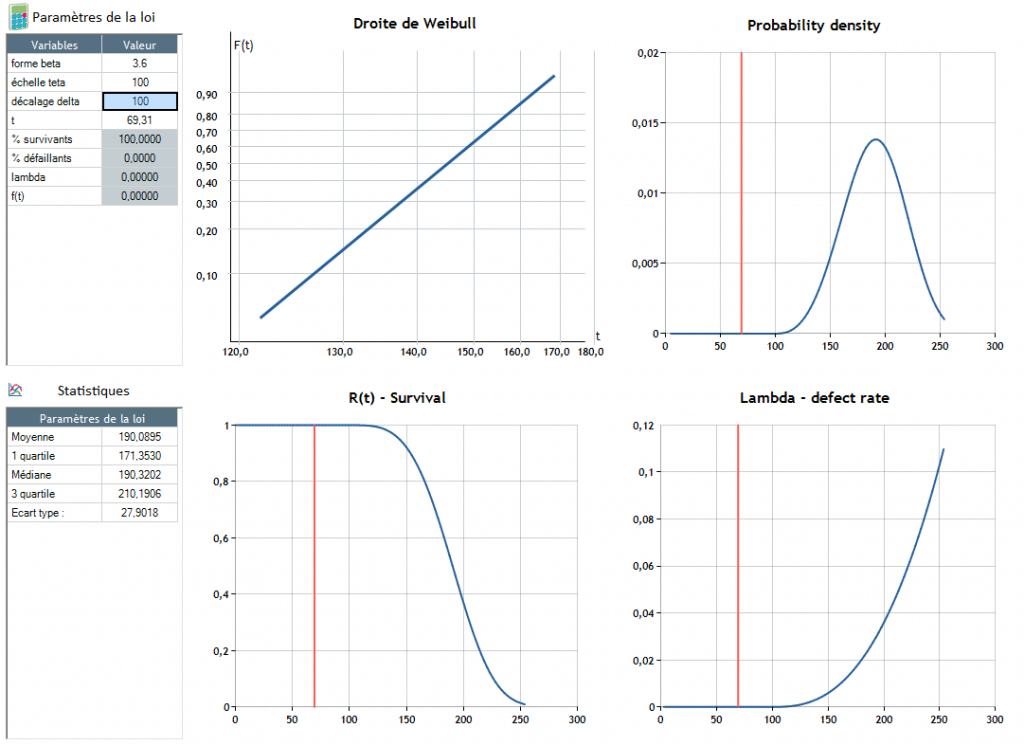
Β = 3,6 - θ = 100, δ = 100
El fallo se produce alrededor de t = 190,4