Para explicar el teorema central del límite, tomemos esto como punto de partida. Dios no juega a los dados", dijo una vez A.Einstein sobre la mecánica cuántica, poniendo en tela de juicio uno de los fundamentos de la física moderna. Sin embargo, los experimentos realizados en el siglo XX demostraron que estaba equivocado, y ahora se acepta que todos los observables de este mundo se rigen por probabilidades de distribución y están sujetos al principio de incertidumbre de Heisenberg. El mundo es aleatorio...
Comprender los fenómenos aleatorios es fundamental para entender cómo funciona el mundo. Un teorema central del análisis estadístico de datos puede demostrarse matemáticamente: el teorema del límite central.
Cualquier sistema resultante de la suma de muchos factores, independientes entre sí y de un orden de magnitud equivalente, genera una ley de distribución que tiende a una distribución normal.
Este teorema muestra la importancia de la distribución normal para analizar la variabilidad de un observable. Para ilustrarlo, lancemos un dado 1000 veces seguidas y observemos la distribución de los resultados:

La distribución sigue una distribución uniforme, es decir, hay la misma probabilidad de que el dado caiga en 1, 2, 3, 4, 5 ó 6. La distribución no se parece a una distribución normal.
Tiremos 10 dados 1000 veces seguidas y veamos cómo se distribuye la suma de estos 10 dados:
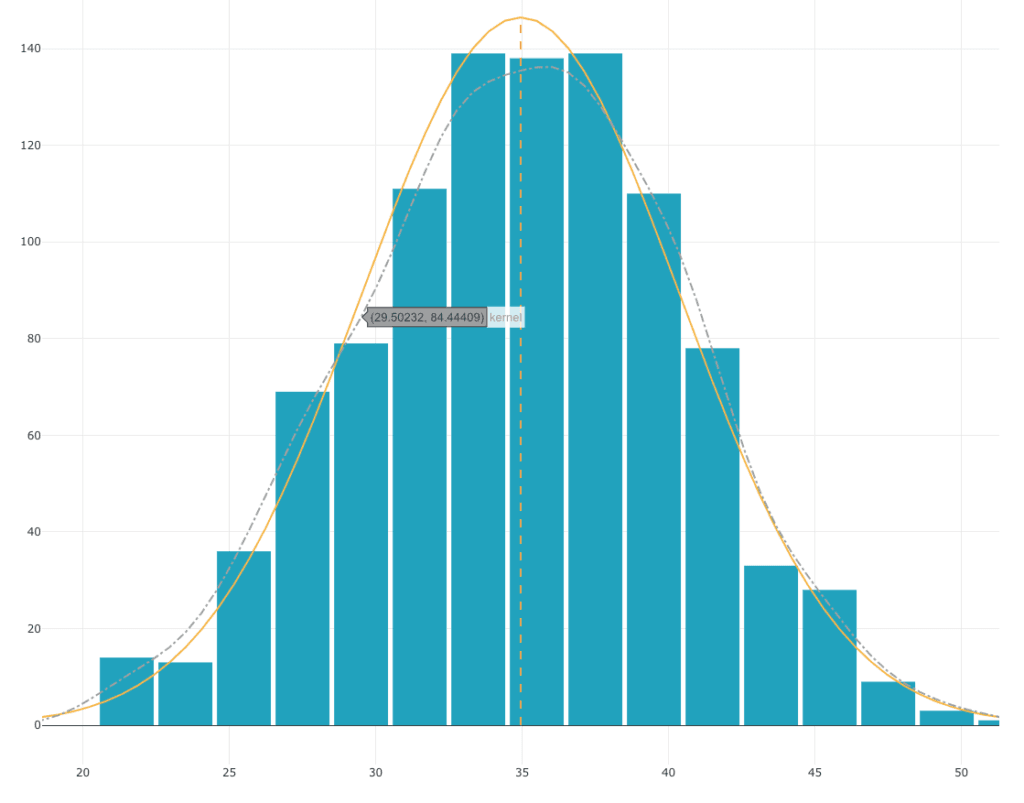
Aunque cada uno de los dados sigue una distribución uniforme, la distribución de la suma de los 10 dados sigue una curva de campana. Esta distribución se aproxima mucho a una distribución normal.
De hecho, si seguimos el teorema central del límite :
- Tenemos un sistema
- Resultado de la suma de muchos factores (en este caso la suma de 10 dados)
- Independientes entre sí (el resultado de un dado no influye en el resultado de otro dado)
- El orden de magnitud de cada uno de los dados es equivalente
La distribución generada por este sistema tiende hacia una distribución normal. En general, esto es bastante intuitivo. Cuando se lanzan 10 dados, sólo hay una combinación que producirá un resultado de 10 (todos los dados cayeron en 1), mientras que hay miles de combinaciones que producirán un resultado de 35. Como consecuencia, es mucho más probable que se produzcan resultados cercanos a 35 que resultados extremos como 10 o 60. Por lo tanto, es mucho más probable que se produzcan resultados cercanos a 35 que resultados extremos como 10 o 60. Por lo tanto, la ley de distribución obtenida se aproxima a una ley de distribución normal.
Los sistemas que observamos habitualmente tienen este tipo de distribución, porque cumplen los supuestos del teorema central del límite. Tomemos el ejemplo del mecanizado de una pieza:
- Es un sistema que produce una característica.
- La desviación de la característica respecto al objetivo es el resultado de la suma de muchos factores (vibraciones, dureza del material, error de posicionamiento de la herramienta, etc. ....).
- Los factores son independientes entre sí (las vibraciones de la máquina no influyen en la dureza del material).
- El orden de magnitud de estas desviaciones equivale a
Por tanto, la distribución de las piezas tiende a una distribución normal, que es lo que observamos cuando medimos una serie de piezas.
