Pour expliquer le théorème central limite, prenons comme point de départ ceci. Dieu ne joue pas aux dés, disait un jour A.Einstein à propos de la mécanique quantique, remettant en question une des bases de la physique moderne. Pourtant, les expériences menées au XXème siècle lui ont donné tort et il est désormais admis que l’ensemble des observables de ce monde régissent selon des probabilités de distribution et sont soumis au principe d’incertitude d’Heisenberg. Le monde est aléatoire…
La compréhension des phénomènes aléatoires est fondamentale pour comprendre comment fonctionne le monde. Or, on peut démontrer mathématiquement un théorème central de l’analyse statistique des données : le théorème centrale limite.
Tout système, résultant de la somme de nombreux facteurs, indépendants les uns des autres et d’un ordre de grandeur équivalent, génère une loi de répartition qui tend vers une loi normale.
Ce théorème montre l’importance de la loi normale dans l’analyse de la variabilité d’une observable. Pour l’illustrer, lançons un dé 1000 fois de suite et observons la répartition des résultats :

La répartition suit une loi uniforme, c’est-à-dire qu’il y a autant de chances que le dé tombe sur 1, 2, 3, 4, 5 ou 6. La loi de répartition ne ressemble pas à une loi normale.
Lançons cette fois-ci 10 dés 1000 fois de suite et observons la répartition des résultats de la somme de ces 10 dés :
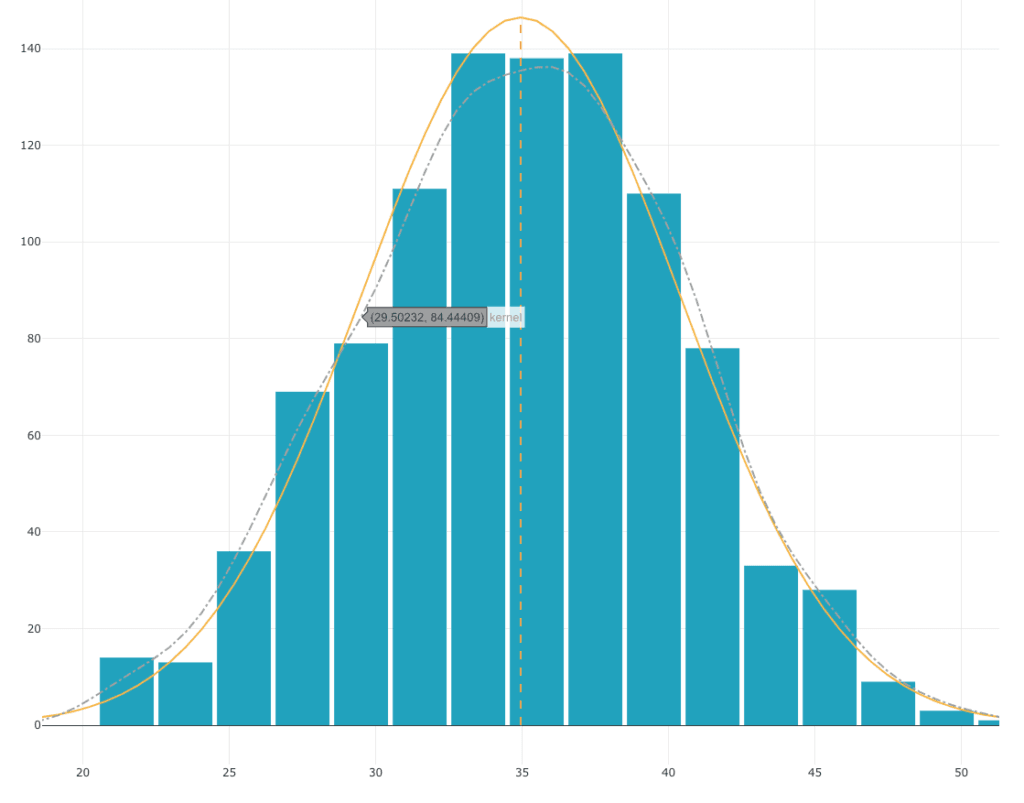
Bien que chacun des dés suit une loi de répartition uniforme, la distribution de la somme des 10 dés suit une courbe en cloche. Cette loi de répartition est très proche d’une loi normale.
En effet, si l’on suit ce que donne le théorème centrale limite :
- Nous avons un système
- Résultant de la somme de nombreux facteurs (ici la somme de 10 dés)
- Indépendants les uns des autres (le résultat d’un dé n’a pas d’influence sur le résultat d’un autre dé)
- L’ordre de grandeur de chacun des dés est équivalent
La distribution générée par ce système tend bien vers une loi normale. Cela est, somme toute, assez intuitif. Lorsque l’on lance 10 dés il n’existe qu’une seule combinaison qui donnera comme résultat 10 (tous les dés sont tombés sur 1), alors qu’il existe des milliers de combinaisons qui donneront comme résultat 35. Par suite, les résultats proches de 35 ont beaucoup plus de probabilités de se produire que les résultats extrêmes comme 10 ou 60. La loi de répartition obtenue est donc proche d’une loi de répartition normale.
C’est ce que l’on retrouve en général, les systèmes que nous observons habituellement ont ce type de distribution, car ils répondent aux hypothèses du théorème central limite. Prenons l’exemple de l’usinage d’une pièce :
- Il s’agit d’un système qui produit une caractéristique.
- La déviation de la caractéristique par rapport à la cible résulte de la somme de nombreux facteurs (vibrations, dureté de la matière, erreur de positionnement de l’outil, etc….)
- Les facteurs sont indépendants les uns des autres (les vibrations de la machine n’ont pas d’influence sur la dureté de la matière)
- L’ordre de grandeur de ces déviations est équivalent
La distribution des pièces tend donc vers une loi normale, c’est ce que l’on observe lorsque l’on mesure une série de pièces.
