Dans cette article nous allons voir comment calculer les différents indices de capabilité et notamment les indices Cp, Pp et Ppk.
Pour bien apprécier la capabilité d’un processus la notion de temps est particulièrement importante car on différencie deux types de variabilité :
- La variabilité court-terme : lorsque l’on produit deux pièces consécutivement, ces deux pièces ne seront pas tout à fait équivalentes à causes des variations intrinsèques de la machine. Cette variabilité court-terme dépend principalement de la machine.
- La variabilité long-terme : lorsque l’on produit sur un même process pendant une plus longue période, la machine elle-même va se dérégler, les changements de série, le changement de lot matière etc… vont apporter de nouvelles sources de variation. Cette variabilité long-terme dépend de la machine mais également de nombreuses sources de variabilité extérieures et de la manière de piloter le process.
Exemple
Pour illustrer ce propos, observons le schéma de production suivant :
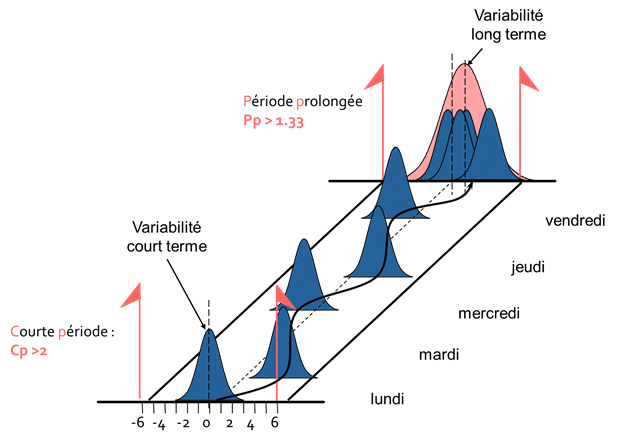
La production de la semaine est le résultat de la production des différents jours de la semaine. Or comme l’illustre le schéma ci-dessus, les conditions de production entre les différents jours de la semaine ne sont pas équivalentes. Le centrage du procédé n’est pas le même entre la production de lundi, mardi, etc…
Par suite, on observe que la variabilité sur l’ensemble de la semaine (courbe rouge) est plus importante que la variabilité que l’on observe sur une faible période de temps car elle prend en compte moins de phénomènes pouvant provoquer de la variabilité comme un réglage ou un changement de matière.
Il y a donc deux manières de caractériser la capabilité d’un process, selon le type de variabilité que l’on observe : le court terme cp et le long terme pp.
Indice de Capabilité court terme Cp
Court terme Cp: La capabilité court terme permet de caractériser l’aptitude du process à produire des pièces bonnes en ne prenant en compte que la variabilité intrinsèque du process (la variabilité entre deux pièces consécutives. La capabilité court terme est notée Cp et se calcule par :
Cp=\frac{\text{tolerance interval}}{6*\text{short term dispersion}}= \frac{\text{tolerance interval}}{6*\sigma_{\text{short term}}}
En général, on souhaite :
Cp > 2
Indice de capabilité long terme Pp
Long terme Pp: La capabilité long terme permet de caractériser l’aptitude du process à produire des pièces bonnes sur une longue période de temps, c’est-à-dire en prenant en compte les réglages et les modification de process qui peuvent avoir lieu. La capabilité long terme est notée Pp et se calcule par :
Pp=\frac{tolerance interval}{6∗long term dispersion}=\frac{tolerance interval}{6∗σ_{long term}}
En général, on souhaite :
Pp > 1.33
La capabilité long-terme, prenant en compte plus de sources de variabilité que pour le court-terme, on a forcément :
\text{long term dispersion} < \text{short term dispersion}
Et donc
Pp < Cp
Si, ce n’est pas le cas, cela ne signifie pas que la dispersion court terme est plus importante que la dispersion long terme, mais que la dispersion n’est pas stable au cours du temps.
Les méthodes pour calculer les indices de capabilité Cp, Pp, Ppk
Comme nous venons de le voir, on calcule le Cp et Pp selon la même formule. On différencie le Cp et le Pp avec les périodes de temps sur laquelle la variabilité est calculée. Il y a plusieurs méthodes pour calculer Cp et Pp.
Méthode 1 : En réalisant plusieurs prélèvements à intervalle régulier
La première méthode pour calculer les variabilités court-terme et long-terme est de réaliser plusieurs prélèvements à intervalle régulier.
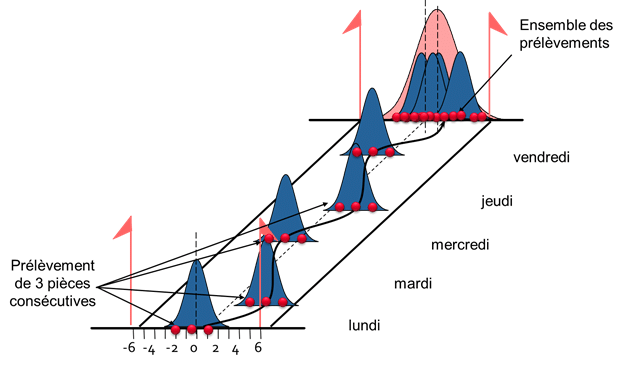
Variabilité court-terme : on calcule la variabilité court-terme en utilisant le calcul de l’écart-type intra-série de l’ensemble des prélèvements :
\sigma_{\text{short term}}=\sigma_{\text{intra sample}}
Variabilité long-terme : on prélève 50 pièces réparties sur une période caractéristique du process, pour prendre en compte de multiples sources de variation du process comme des réglages, des changements d’outils, de matière, etc… La variabilité long-terme est calculée par :
\sigma_{\text{long term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}
Exemple : On réalise le prélèvement suivant
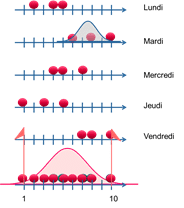
L’intervalle de tolérance est [1 ;10].
On calcule l’écart-type intra-série :
\sigma_{\text{short term}}=\sigma_{\text{intra sample}}=1.7321
On calcule l’écart-type de toutes les pièces :
\sigma_{\text{long term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}=2.6904
On en déduit donc :
Cp=\frac{\text{tolerance interval}}{6*\text{short term dispersion}}= \frac{\text{tolerance interval}}{6*\sigma_{\text{short term}}}=\frac{9}{6*1.7321}=0.87
Pp=\frac{\text{tolerance interval}}{6*\text{long term dispersion}}= \frac{\text{tolerance interval}}{6*\sigma_{\text{long term}}}=\frac{9}{6*2.6904}=0.56
Ppk=\frac{Min(\text{tolerance max}-\mu,mu-\text{tolerance min})}{3*\text{long term dispersion}}= \frac{4.33}{3*2.6904}=0.54
Méthode 2 : En réalisant deux prélèvements distincts
La seconde méthode pour calculer les variabilités court-terme et long-terme est de réaliser deux prélèvements distincts.
- Variabilité court-terme : on prélève 50 pièces consécutives sans réglage pour permettre de calculer la variabilité court-terme du process. La variabilité court-terme est calculée par :
\sigma_{\text{short term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}
- Variabilité long-terme : on prélève 50 pièces réparties sur une période caractéristique du process, pour prendre en compte de multiples sources de variation du process comme des réglages, des changements d’outils, de matière, etc… La variabilité long-terme est calculée par :
\sigma_{\text{long term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}

