The Weibull distribution is most often used to model reliability data. Ellistat's Data Analysis module allows you to perform these analyses with ease.
Definitions: Reliability, the Weibull Distribution, Failure
Reliability:
Reliability is the ability of an entity to perform a required function, under given conditions, during a given time interval.
Failure:
Failure is the end of a device's ability to perform an expected function. It may be partial (deterioration in performance) or total (end of function).
R(t)Probability that an entity E is non-defaulting over the time span [0 ; t ], assuming it is non-defaulting at time t = 0.
F(t)F(t) is the cumulative function of failures è F(t) = 1 - R(t)
Probability density f(t) represents the product failure rate, i.e. the probability that a product will fail over the time interval [t,t+dt].
????(????)=number of deˊfailing eˊlements over timeΔ????number of eˊleˊments testeˊsf(t)=number of eˊleˊments testeˊsnumber of deˊfailing eˊlements over a timeΔt
λ(t) or failure rate : λ(t) represents the product failure rate, i.e. the probability that a product will fail over the time interval [t,t+dt] knowing that it did not fail at time t.
????(????)=number of eˊleˊments deˊfaillant over a timeΔ????number of eˊlements deˊfaillants still in testingλ(t)=number of failing eˊlements still in testnumber of eˊleˊments failing over a timeΔt
- λ(t) decreases Defect rate decreases over time, generally corresponding to early defects. Products with intrinsic defects deteriorate rapidly, while other products last much longer.
- λ(t) constant The failure rate does not depend on time. There is just as much risk of a product failing at time t, whatever its lifetime. These are intrinsic failures. This is the type of failure often found in electronic products.
- λ(t) increases The failure rate increases over time. The risk of a product failing increases with the product's lifespan. This is the end of the product's life.
MTTF (Mean Time To Failure)
The MTTF, more commonly used in Product Reliability, is the average time to first failure.
MTBF (Mean Time Between Failure)
MTBF (Mean Time Between Failures) is the average of the time intervals between two failures.
The Weibull Distribution
To model a product's failure rate, you need to be able to model multiple types of failure:
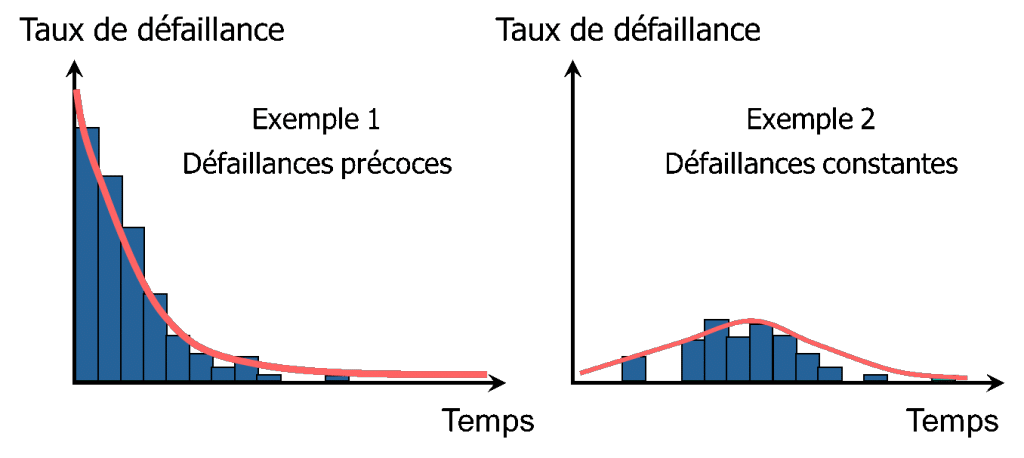
For this reason, the Weibull distribution is mainly used, as it allows for great variability in shape.
Thanks to its great flexibility, the Weibull distribution can be used to model the behavior of many types of failure, such as:
- The breaking strength of components or the effort required to fatigue metals
- The failure time of an electronic component
- Failure time for items used outdoors, such as car tires
- Systems that fail when the weakest component in the system fails
The Weibull distribution can also be used to model the behavior of different life situations of the same component.
The Weibull distribution function is as follows:
R\left( t \right)=e-\left( \frac{t-\delta}{\phi} \right)^{\beta}
It has 3 parameters:
- ????: shape parameter
- θ : scaling parameter
- ????: delay parameter
β: shape parameter
It allows the shape of the distribution to be adapted to be as close as possible to the observed failure rate:
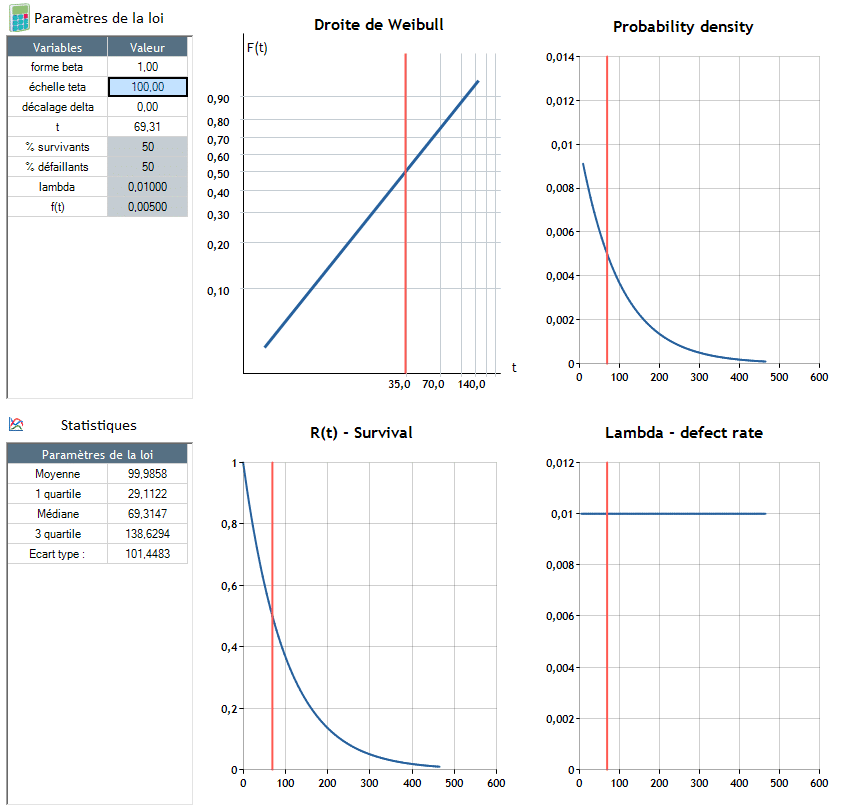
β=1: Failure rate is constant (λ constant)
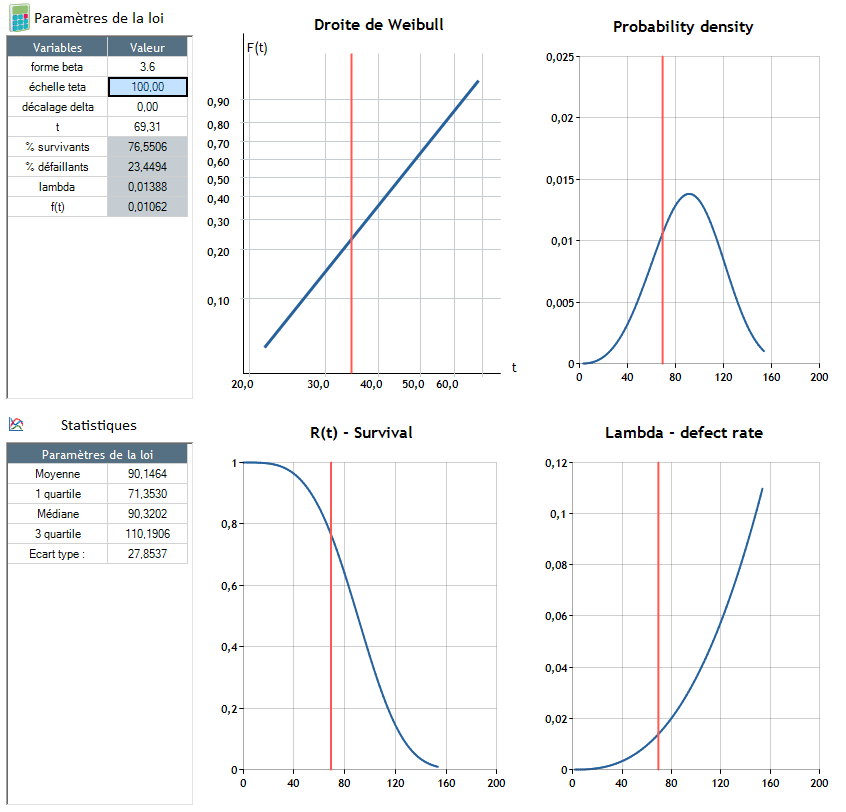
β>1: Failure rate increases over time (λ increases - product end-of-life)
θ: scaling parameter
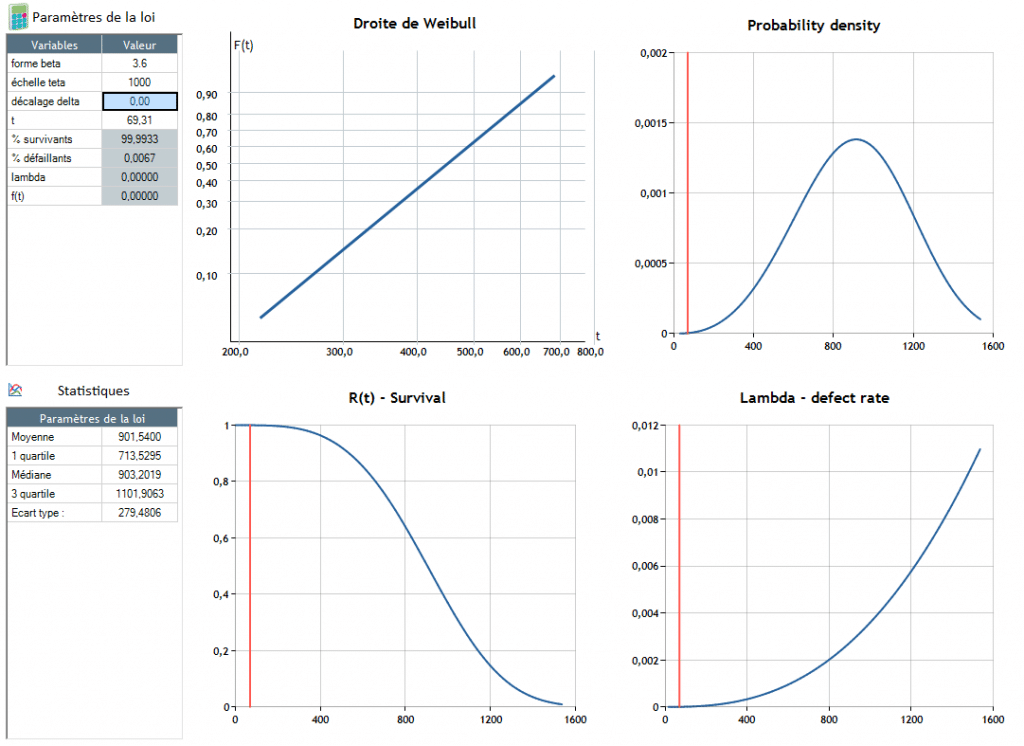
The parameter θ is used to adjust the scale of the distribution law to the scale of the problem found, for example :
Failure occurs around t = 90.4
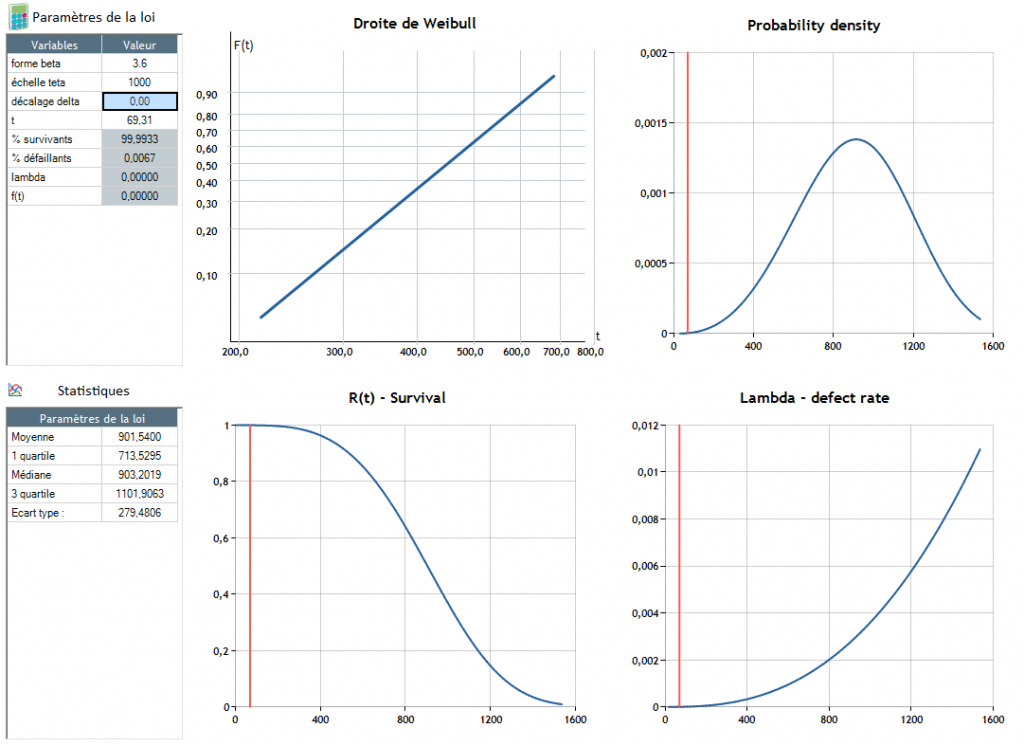
Failure occurs around t = 904
δ: delay parameter
The parameter δ allows the distribution to be shifted by one parameter δ
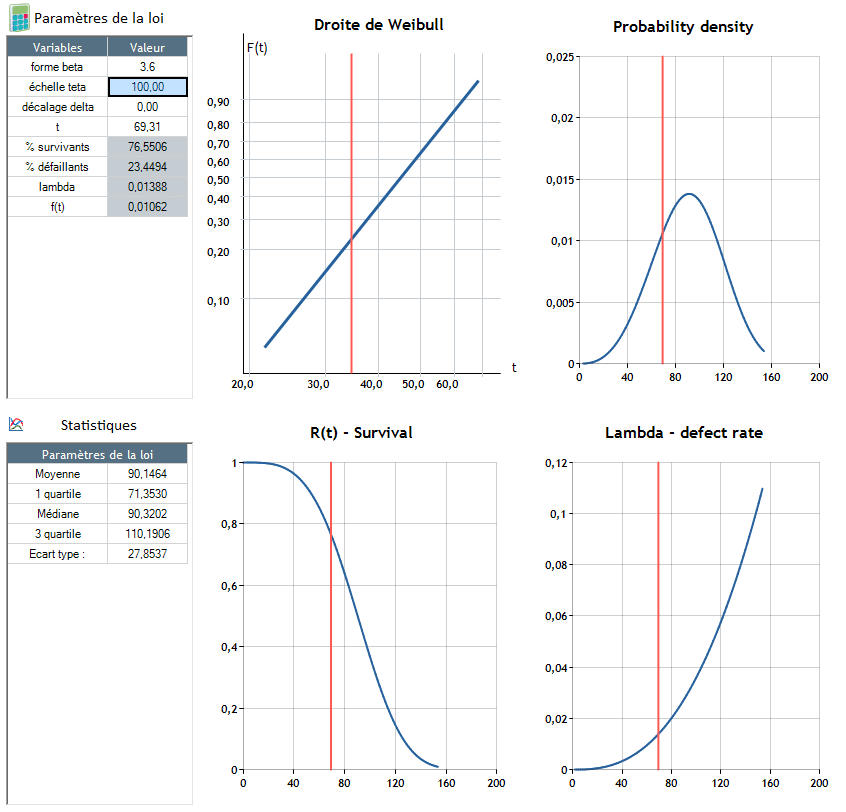
Β = 3.6 - θ = 100, δ = 0
Failure occurs around t = 90.4
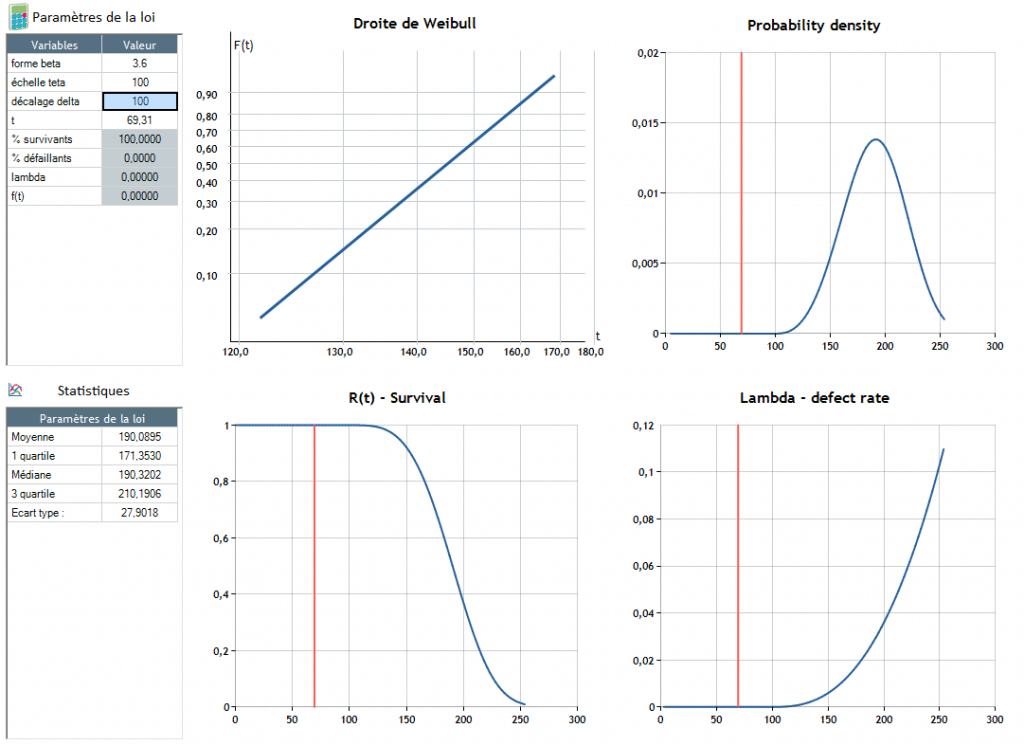
Β = 3.6 - θ = 100, δ = 100
Failure occurs around t = 190.4
