La garantía R&R se utiliza para cualificar un proceso de medición. Esto significa comprobar que la variabilidad del proceso de medición es compatible con la variabilidad de la magnitud que se va a medir.
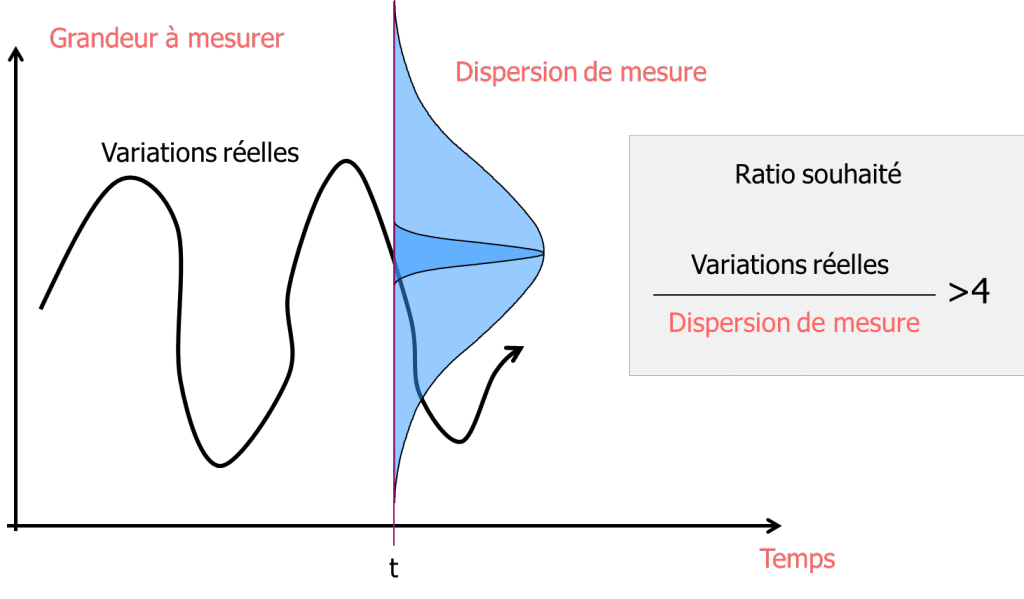
Se considera necesaria una relación de 4 entre la variabilidad de las piezas y la variabilidad de la medición. Esta relación se expresa como producción Cpc:
\text{producción CPC}=\frac{text{dispersión de la producción}}{text{dispersión de la medición}}
Por tanto, la Cpc de producción depende de la dispersión de las piezas. Sin embargo, cuando queremos caracterizar un instrumento de medida, deseamos que esta caracterización sea independiente de la variabilidad de la producción. Por tanto, vamos a introducir un nuevo tipo de variable que nos permita caracterizar el instrumento de medida no en términos de dispersión de las piezas, sino en términos de intervalo de tolerancia de las piezas.
Del mismo modo que se calcula una capacidad, se caracterizará el instrumento de medida:
- O por Cpc (Capacidad de Proceso de Control):
\text{Cpc}=\frac{\text}{intervalo de tolerancia}}{\text}{dispersión de la medida}}> 4
- GRR% (Repetibilidad y reproducibilidad):
{\text{GRR}}= {\frac{text{dispersión de la medida}} {\text{intervalo de tolerancia}}<\text{0,3}}
Como puede ver, los dos indicadores representan lo mismo y tenemos la relación :
\text{GRR}=\frac{\text{1}}{\text{Cpc}}
Estas son las normas generalmente aceptadas:
| Cpc | GRR% | |
|---|---|---|
| Inaceptable | <3 | >30% |
| Proceso límite | >3 y < 4 | 20% |
| Aceptable | >4 | <20% |
| Excelente | >8 | <10% |
Cálculo de la dispersión de un instrumento de medida
Para calcular la dispersión de un proceso de medición, se utiliza una prueba de repetibilidad y reproducibilidad.
La prueba de repetibilidad y reproducibilidad tiene por objeto caracterizar la dispersión global del proceso de medición separando lo que es repetibilidad (es decir, la dispersión de la repetición de la medición) de lo que es reproducibilidad (es decir, la diferencia entre varios operadores).
Para realizar esta prueba necesitas :
Prueba estándar: 3 operarios miden 10 partes 3 veces cada uno
Prueba rápida: 3 operadores miden cada uno 10 partes 1 vez cada uno (esta prueba no separa la repetibilidad y la reproducibilidad)
Una vez realizadas las mediciones, existen dos métodos para calcular la dispersión del medio de medición:
Método ANAVAR : Un método más preciso, que calcula la repetibilidad y la reproducibilidad y detecta si hay interacciones entre piezas y operarios.
Método RANGE : Un método más aproximado, fácil de calcular con una hoja de cálculo Excel, pero que no detecta ninguna interacción pieza/operador.
Le recomendamos que mantenga el método de cálculo ANAVAR, ya que es el más preciso.
Método de la gama
El método de rangos se utiliza sobre todo en la industria porque sus cálculos pueden hacerse fácilmente a mano.
Este método puede utilizarse para calcular la repetibilidad y la reproducibilidad del proceso de medición. Sin embargo, no permite calcular la interacción, lo que limita su alcance. Los cálculos de este método se basan en el cálculo de una desviación típica intramuestra de los rangos.
El principio de cálculo es el siguiente:
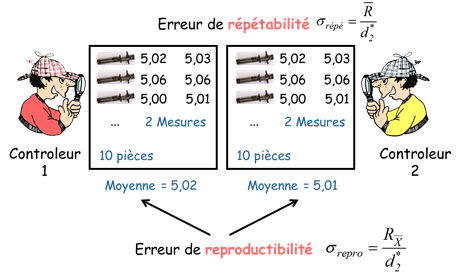
Todas las mediciones de cada pieza realizadas por cada operario se consideran una muestra. De este modo, la variabilidad intramuestra representa la repetibilidad del proceso de medición, que se calcula mediante :
\sigma_{repetablity}=\frac{\overline{R}}{d_{2}^{*}}
A continuación, consideramos las medias de las mediciones de cada operador como una muestra. Esto permite calcular la reproducibilidad del proceso de medición mediante :
\sigma_{operator}=\frac{R_{\overline{X}}}{d_{2}^{*}}
Método ANAVAR
La Método ANAVAR es más compleja:
Para calcular la GRR y la Cpc con el método ANAVAR, utilizamos el test de Fisher:
| Fuentes de variabilidad | Suma de cuadrados | Grado de libertad | Cuadrado medio | Estadística F |
|---|---|---|---|---|
| Operador | SSA | a-1 | \text{MSA}=\frac{\text{SSA}}{\text{a-1}} | \text{F}=\frac{\text{MSA}}{\text{MSE}} |
| Piezas | BLU | b-1 | \text{MSB}=\frac{\text{SSB}}{\text{b-1}} | \text{F}=\frac{\text{MSB}}{\text{MSE}} |
| Interacción (Operador/parte) | SSAB | (a-1)(b-1) | \text{MSAB}=\frac{\text{SSAB}}{\text{(a-1)(b-1)}} | \text{F}=\frac{\text{MSAB}}{\text{MSE}} |
| Instrumento | ESS | ab(n-1) | \text{MSE}=\frac{\text{SSE}}{\text{ab(n-1)}} | |
| Total | TSS | N-1 |
con:
- a = número de operadores
- b = número de piezas
- n = número de repeticiones
- N = número total de mediciones = abn
\text{SSA}=\sum^{a}{\frac{Y_{i}^{2}}{\text{bn}}}-\frac{Y_{**}^{2}}{N}
\text{SSB}=\sum^{b}{\frac{Y_{i}^{2}}{\text{an}}}-\frac{Y_{**}^{2}}{N}
\text{SSAB}=\sum^{a}\sum^{b}{\frac{Y_{ij}^{2}}{n}}-\frac{Y_{**}^{2}}{N}-\text{SSA}-\text{SSB}
\text{TSS}=\sum^{a}\sum^{b}\sum^{n}Y_{ijk}^{2}-\frac{Y_{**}^{2}}{N}
\text{SSE}=\text{TSS}-\text{SSA}-\text{SSB}-\text{SSAB}
La repetibilidad del proceso de medición viene dada por :
\text{Répétabilité}=5.15\sqrt{\text{MSE}}
La reproducibilidad del proceso de medición viene dada por :
\text{Reproductibilité}=5.15\sqrt{\frac{\text{MSA}-\text{MSAB}}{\text{bn}}}
La interacción viene dada por :
\text{Intéraction}=5.15\sqrt{\frac{\text{MSAB}-\text{MSE}}{\text{n}}}
La variabilidad del proceso de medición viene dada por
\text{Dispersión}=5.15\sqrt{text{Repetibilidad}^2+text{Reproducibilidad}^2+text{Interpretación}^2}
Por último, calculamos :
\text{GRR}=frac{Dispersión}{IT}
Este método es, por tanto, mucho más complejo de aplicar, pero permite calcular la interacción como fuente de dispersión, lo que no es posible con el método RANGE. Por lo tanto, es más preciso.