Le gage R&R permet de qualifier un processus de mesure. C’est-à-dire vérifier que la variabilité du processus de mesure est compatible avec la variabilité de la quantité à mesurer.
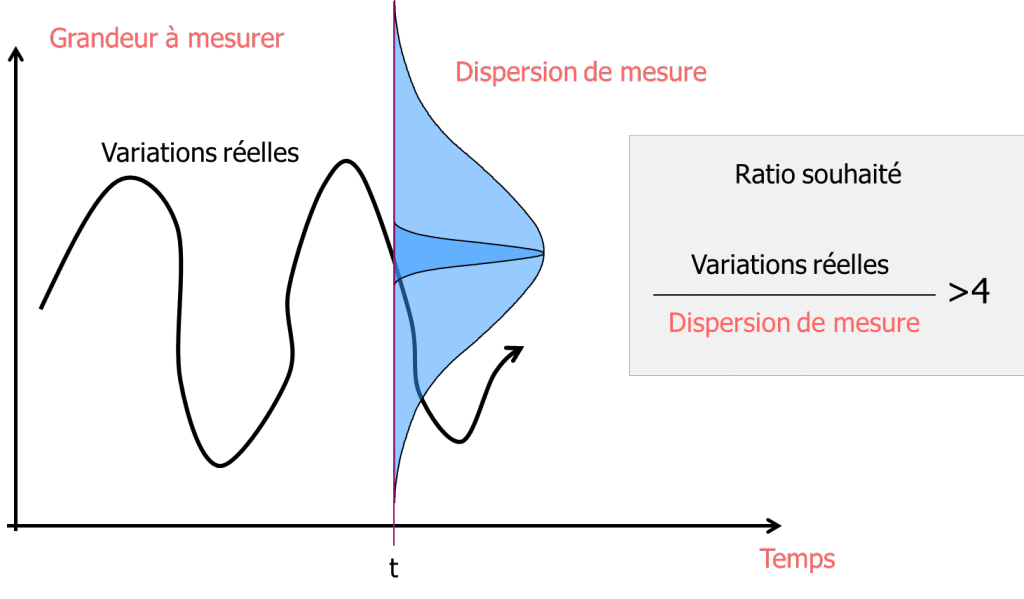
On considère qu’il est nécessaire d’avoir un ratio de 4 entre la variabilité des pièces et la variabilité de la mesure. Ce ratio s’exprime sous le nom de Cpc production :
\text{Cpc production}=\frac{\text{production dispersion}}{\text{measurement dispersion}}
Le Cpc production dépend donc de la dispersion des pièces. Or, lorsque l’on veut caractériser un instrument de mesure, on souhaiterait que cette caractérisation soit indépendante de la variabilité de la production. Nous allons donc introduire un nouveau type de variable, qui permet de caractériser l’instrument de mesure non pas par rapport à la dispersion de pièce mais par rapport à l’intervalle de tolérance des pièces.
De la même manière que l’on calcule une capabilité, l’instrument de mesure sera caractérisé :
- Soit par le Cpc (Capabilité du Processus de Contrôle) :
\text{Cpc}=\frac{\text{tolerance interval}}{\text{measurement dispersion}}> 4
- Soit par le GRR% (Répétabilité et Reproductibilité) :
{\text{GRR}=\frac{\text{measurement dispersion}}{\text{tolerance interval}}<\text{0.3}}
Comme vous pouvez le remarquer, les deux indicateurs représentent la même chose et l’on a la relation :
\text{GRR}=\frac{\text{1}}{\text{Cpc}}
Voici donc les règles habituellement admises :
| Cpc | GRR% | |
|---|---|---|
| Inacceptable | <3 | >30% |
| Processus limite | >3 et < 4 | <30% et >20% |
| Acceptable | >4 | <20% |
| Excellent | >8 | <10% |
Calculer la dispersion d’un instrument de mesure
Pour calculer la dispersion d’un processus de mesure, on utilise un test de répétabilité et reproductibilité.
Le test de répétabilité et reproductibilité vise à caractériser l’ensemble de la dispersion du processus de mesure en séparant ce qui est du ressort de la répétabilité (c’est-à-dire la dispersion de la répétition de mesure) de ce qui est du ressort de la reproductibilité (c’est-à-dire une différence entre plusieurs opérateurs).
Pour réaliser ce test il faut :
Test standard : 3 opérateurs mesurent chacun 10 pièces 3 fois chacune
Test rapide : 3 opérateurs mesurent chacun 10 pièces 1 fois chacune (ce test ne permet pas de dissocier répétabilité et reproductibilité)
Une fois les mesures effectuées, il y a deux méthodes pour calculer la dispersion du moyen de mesure :
Méthode ANAVAR : Méthode plus exacte, qui permet de calculer à la fois la répétabilité, la reproductibilité et détecter s’il y a des interactions entre pièces et opérateurs.
Méthode RANGE : Méthode plus approchée, facile à calculer avec un tableur Excel, mais qui ne permet pas de détecter une éventuelle interaction pièces/opérateur.
Nous vous recommandons de conserver la méthode de calcul ANAVAR car c’est la plus précise
Méthode Range
La méthode range est particulièrement utilisée dans l’industrie car ses calculs peuvent être facilement réalisé à la main.
Cette méthode permet de calculer la répétabilité et reproductibilité du processus de mesure. Cependant, elle ne permet pas de calculer l’interaction, ce qui limite sa portée. Les calculs de cette méthode sont basés sur le calcul d’un écart type intra-échantillon à partir des étendues.
Le principe de calcul est le suivant :
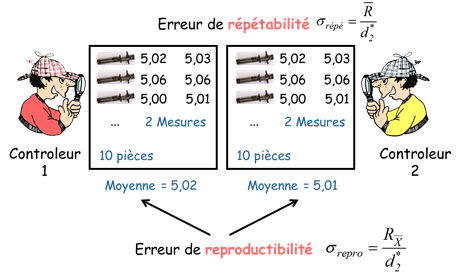
On considère l’ensemble des mesures de chaque pièce par chaque opérateur comme étant un échantillon. De cette manière, la variabilité intra-échantillon représente la répétabilité du processus de mesure, que l’on calcule par :
\sigma_{repetablity}=\frac{\overline{R}}{d_{2}^{*}}
On considère ensuite, les moyennes des mesures de chaque opérateur comme étant un échantillon. Cela qui permet de calculer la reproductibilité du processus de mesure par :
\sigma_{operator}=\frac{R_{\overline{X}}}{d_{2}^{*}}
Méthode ANAVAR
La méthode ANAVAR est plus complexe:
Pour calculer le GRR et le Cpc en utilisant la méthode ANAVAR on utilise les analyses statistiques du test de Fisher :
| Sources de variabilité | Somme des carrés | Degré de liberté | Moyenne des carrés | F-Statistique |
|---|---|---|---|---|
| Opérateur | SSA | a-1 | \text{MSA}=\frac{\text{SSA}}{\text{a-1}} | \text{F}=\frac{\text{MSA}}{\text{MSE}} |
| Pièces | SSB | b-1 | \text{MSB}=\frac{\text{SSB}}{\text{b-1}} | \text{F}=\frac{\text{MSB}}{\text{MSE}} |
| Interaction (Opérateur/pièce) | SSAB | (a-1)(b-1) | \text{MSAB}=\frac{\text{SSAB}}{\text{(a-1)(b-1)}} | \text{F}=\frac{\text{MSAB}}{\text{MSE}} |
| Instrument | SSE | ab(n-1) | \text{MSE}=\frac{\text{SSE}}{\text{ab(n-1)}} | |
| Total | TSS | N-1 |
avec:
- a = nombre d’opérateurs
- b = nombre de pièces
- n = nombre de répétitions
- N = nombre total de mesures = abn
\text{SSA}=\sum^{a}{\frac{Y_{i}^{2}}{\text{bn}}}-\frac{Y_{**}^{2}}{N}
\text{SSB}=\sum^{b}{\frac{Y_{i}^{2}}{\text{an}}}-\frac{Y_{**}^{2}}{N}
\text{SSAB}=\sum^{a}\sum^{b}{\frac{Y_{ij}^{2}}{n}}-\frac{Y_{**}^{2}}{N}-\text{SSA}-\text{SSB}
\text{TSS}=\sum^{a}\sum^{b}\sum^{n}Y_{ijk}^{2}-\frac{Y_{**}^{2}}{N}
\text{SSE}=\text{TSS}-\text{SSA}-\text{SSB}-\text{SSAB}
La répétabilité du processus de mesure est donnée par :
\text{Répétabilité}=5.15\sqrt{\text{MSE}}
La reproductibilité du processus de mesure est donnée par :
\text{Reproductibilité}=5.15\sqrt{\frac{\text{MSA}-\text{MSAB}}{\text{bn}}}
L’interaction est donnée par :
\text{Intéraction}=5.15\sqrt{\frac{\text{MSAB}-\text{MSE}}{\text{n}}}
La variabilité du processus de mesure est donnée par
\text{Dispersion}=5.15\sqrt{\text{Répétabilité}^2+\text{Reproductibilité}^2+\text{Intéraction}^2}
On calcule enfin :
\text{GRR}=\frac{Dispersion}{IT}
Cette méthode est donc beaucoup plus complexe à mettre en oeuvre, mais elle permet de calculer l’intéraction comme source de dispersion, ce que ne permet pas la méthode RANGE. Elle est donc plus précise.