En este artículo veremos cómo calcular los distintos índices de capacidad, en particular Cp, Pp y Ppk.
Para apreciar plenamente la capacidad de un proceso, la noción de tiempo es especialmente importante, ya que existen dos tipos de variabilidad:
- Variabilidad a corto plazo: cuando se fabrican dos piezas consecutivas, estas dos piezas no serán completamente equivalentes debido a las variaciones intrínsecas de la máquina. Esta variabilidad a corto plazo depende principalmente de la máquina.
- Variabilidad a largo plazo: cuando se produce el mismo proceso durante un periodo de tiempo más largo, la propia máquina se desajustará, y los cambios en las series, los cambios en los lotes de material, etc. traerán nuevas fuentes de variación. Esta variabilidad a largo plazo depende de la máquina, pero también de numerosas fuentes externas de variabilidad y de la forma en que se gestiona el proceso.
Ejemplo
Para ilustrar este punto, veamos el siguiente diagrama de producción:
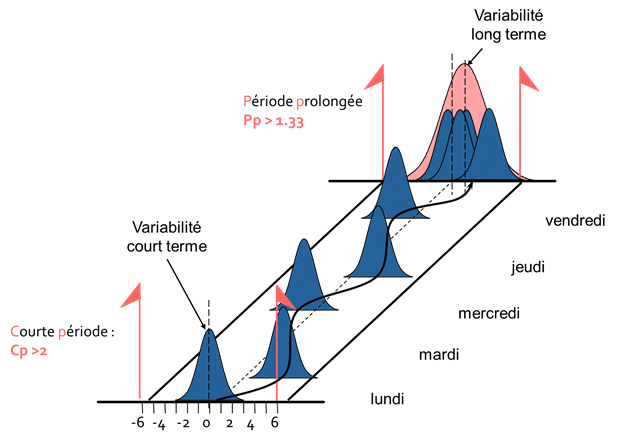
La producción de la semana es el resultado de la producción de los distintos días de la semana. Sin embargo, como ilustra el diagrama anterior, las condiciones de producción en los distintos días de la semana no son equivalentes. El centrado del proceso no es el mismo entre la producción del lunes, el martes, etc.
Como resultado, podemos ver que la variabilidad a lo largo de toda la semana (curva roja) es mayor que la variabilidad observada en un corto periodo de tiempo, porque tiene en cuenta menos fenómenos que podrían causar variabilidad, como un ajuste o un cambio de material.
Por tanto, existen dos formas de caracterizar la capacidad de un proceso, en función del tipo de variabilidad observada: cp a corto plazo y pp a largo plazo.
Índice de capacidad a corto plazo Cp
Cp a corto plazoCapacidad a corto plazo: La capacidad a corto plazo se utiliza para caracterizar la capacidad del proceso de producir piezas buenas, teniendo en cuenta únicamente la variabilidad intrínseca del proceso (la variabilidad entre dos piezas consecutivas). La capacidad a corto plazo se denomina Cp y se calcula mediante :
Cp= \frac {{intervalo de tolerancia}}{6*{dispersión a corto plazo}}= \frac {{intervalo de tolerancia}}{6*{sigma_{corto plazo}}
En general, queremos :
Cp > 2
Índice de capacidad a largo plazo Pp
Pp a largo plazoCapacidad a largo plazo: La capacidad a largo plazo se utiliza para caracterizar la capacidad del proceso de producir piezas buenas durante un largo periodo de tiempo, es decir, teniendo en cuenta los ajustes y modificaciones del proceso que puedan producirse. La capacidad a largo plazo se denomina Pp y se calcula mediante :
Pp=\frac{intervalo de tolerancia}{6∗dispersión a largo plazo}=\frac{intervalo de tolerancia}{6∗σ_{largo plazo}}
En general, queremos :
Pp > 1,33
Como la capacidad a largo plazo tiene en cuenta más fuentes de variabilidad que la capacidad a corto plazo, tenemos necesariamente :
\text{dispersión a largo plazo} < \text{dispersión a corto plazo}
Y así
Pp < Cp
Si no es así, no significa que la dispersión a corto plazo sea mayor que la dispersión a largo plazo, sino que la dispersión no es estable a lo largo del tiempo.
Métodos de cálculo de los índices de capacidad Cp, Pp, Ppk
Como acabamos de ver, Cp y Pp se calculan con la misma fórmula. Cp y Pp se diferencian por los periodos de tiempo sobre los que se calcula la variabilidad. Existen varios métodos para calcular Cp y Pp.
Método 1: Tomando varias muestras a intervalos regulares
El primer método para calcular la variabilidad a corto y largo plazo consiste en tomar varias muestras a intervalos regulares.
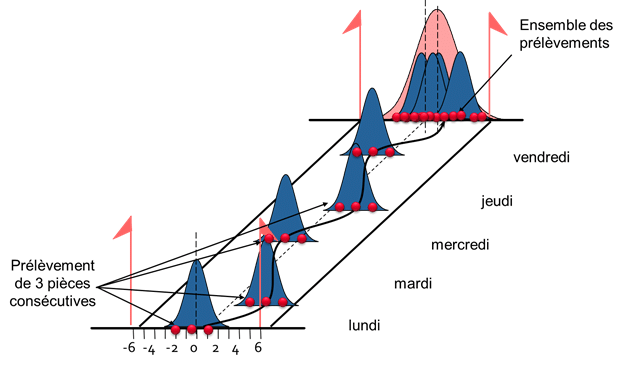
Variabilidad a corto plazo : La variabilidad a corto plazo se calcula utilizando la desviación típica intraserie de todas las muestras:
\Sigma a corto plazo = Sigma dentro de la muestra.
Variabilidad a largo plazo : Se toman muestras de 50 piezas a lo largo de un periodo característico del proceso, para tener en cuenta múltiples fuentes de variación del proceso, como ajustes, cambios de herramientas, cambios de material, etc. La variabilidad a largo plazo se calcula mediante :
\sigma_{\text{long term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}
Ejemplo: Se toma la siguiente muestra
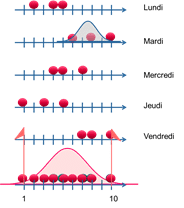
El intervalo de tolerancia es [1 ;10].
Se calcula la desviación típica intraserie :
\sigma_{\text{short term}}=\sigma_{\text{intra sample}}=1.7321
Se calcula la desviación típica de todas las piezas:
\sigma_{\text{long term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}=2.6904
Por tanto, podemos deducir :
Cp= \frac{{intervalo de tolerancia}}{6*texto{dispersión a corto plazo}}= \frac{{intervalo de tolerancia}}{6*sigma_{texto{a corto plazo}}= \frac{9}{6*1,7321}=0,87
Pp= \frac{{intervalo de tolerancia}}{6*texto{dispersión a largo plazo}}= \frac{{intervalo de tolerancia}}{6*sigma_{texto{a largo plazo}}= \frac{9}{6*2,6904}=0,56
Ppk= {\frac{Min(\text{tolerancia máx}-\mu,mu-\text{tolerancia mín})}{3*{texto{dispersión a largo plazo}}= {\frac{4,33}{3*2,6904}=0,54
Método 2: Tomando dos muestras separadas
El segundo método para calcular la variabilidad a corto y largo plazo consiste en tomar dos muestras separadas.
- Variabilidad a corto plazo: se toman 50 piezas consecutivas sin ajustar para calcular la variabilidad a corto plazo del proceso. La variabilidad a corto plazo se calcula mediante :
\sigma_{\text{short term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}
- Variabilidad a largo plazo: se toman muestras de 50 piezas a lo largo de un período característico del proceso, para tener en cuenta múltiples fuentes de variación del proceso, como ajustes, cambios de herramientas, cambios de material, etc. La variabilidad a largo plazo se calcula mediante :
\sigma_{\text{long term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}

