Para comprobar la normalidad, existen varias pruebas que pueden utilizarse para validar o invalidar la hipótesis de que la distribución de las monedas sigue una distribución normal. Las pruebas más utilizadas son :
- La prueba Chi2
- La prueba Anderson-Darling
Prueba de normalidad mediante la prueba Chi2
Para comprobar la normalidad de una distribución, nuestra primera intuición sería trazar el histograma de la distribución de las variables observadas. A continuación, compararíamos si este histograma se parece más o menos a la Curva de Gauss habitual.
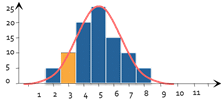
Éste es exactamente el principio en el que se basa la prueba Chi2. Añade a esta intuición una pequeña dosis de cálculo estadístico. El principio es el siguiente:
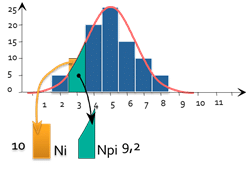
d_i=\frac{(N_i-NP_i)^{2}}{NP_i}
Para cada barra del histograma, podemos calcular :
- Ni : El número de piezas realmente observadas (en este caso 10)
- Npi: El número de partes teóricamente observadas si la distribución fuera normal (aquí 9.2)
- di representa el "número de piezas mal colocadas".
A continuación calculamos
D=suma_{}^{}D_i
y resulta que D sigue una ley de distribución con n-2 grados de libertad (siendo N el número de clases). A continuación, podemos calcular la probabilidad de obtener dicho valor.
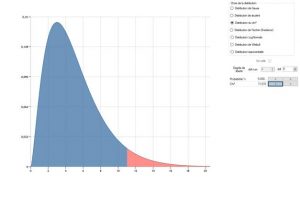
Por ejemplo, para un histograma con 7 clases, si hemos calculado una D de 11,07, calculamos que hay 5% para obtener tal valor o más si la distribución de las partes es efectivamente normal.
Por lo tanto, el resultado de la prueba será 5% y la conclusión general es la siguiente:
- Si X < 5%: se considera que la distribución de las variables no sigue una distribución normal.
- Si X >= 5%: se acepta la hipótesis de normalidad y se puede considerar que la distribución sigue una distribución normal.
Qué hacer en caso de no normalidad
El teorema del límite central nos dice :
Cualquier sistema, resultante de la suma de muchos factores independientes entre sí y de un orden de magnitud equivalente, genera una ley de distribución que tiende a una distribución normal.
Pero también podemos razonar en sentido contrario. Si observamos una distribución que no es normal, entonces una de las hipótesis del teorema no es válida:
- Caso 1: el sistema no es la suma de muchos factores: puede ser el producto de muchos factores u otros. En este caso, la ley de distribución puede ser diferente y, en general, una transformación (tomando el logaritmo del resultado, por ejemplo) restablecerá una distribución normal.
- Caso 2: Los factores no son independientes entre sí
- Caso 3: Los factores no son del mismo orden de magnitud :
- Un factor tiene más peso que los demás. En este caso, tenemos que encontrar el factor en cuestión, porque él solo genera una fuente importante de variabilidad.
- Un valor atípico contamina la distribución. En este caso, tenemos que encontrar la causa del valor atípico y eliminarlo si se puede explicar la causa.
En estos dos casos, no es necesario encontrar una ley de distribución que corresponda a la variabilidad observada. De hecho, esta ley de distribución no será repetible en el tiempo porque se debe a un único parámetro, por lo que no tendrá propiedades predictivas.
Si el origen de la no normalidad se debe al caso 1, deberá encontrar la ley de distribución correspondiente, sobre todo si desea predecir el porcentaje de valores fuera de tolerancia. Para ello, puede utilizar las leyes de distribución propuestas en la parte inferior de la ventana en el módulo Análisis de datos para ver si una de las distribuciones da buena cuenta de los datos observados:

