A Weibull-eloszlást leggyakrabban a megbízhatósági adatok modellezésére használják. Az Ellistat adatelemző modul lehetővé teszi, hogy ezeket az elemzéseket könnyedén elvégezze.
Fogalommeghatározások: megbízhatóság, Weibull-törvény, meghibásodás
Megbízhatóság:
A megbízhatóság egy egység azon képessége, hogy adott körülmények között, adott időintervallum alatt képes egy előírt funkciót ellátni.
Kudarc:
A meghibásodás az eszköz azon képességének megszűnése, hogy az elvárt funkciót elvégezze. A meghibásodás lehet részleges (a teljesítmény csökkenése) vagy teljes (a funkció megszűnése).
R(t)Annak valószínűsége, hogy egy E entitás nem hibás a [0; t ] időszakban, feltételezve, hogy t = 0 időpontban nem hibás.
F(t)F(t) a hibák kumulatív függvénye è F(t) = 1 - R(t)
Valószínűségi sűrűség f(t) a termék meghibásodási rátáját jelenti, azaz annak a valószínűségét, hogy egy termék meghibásodik a [t,t+dt] időintervallum alatt.
λ(t) vagy hibaarány : λ(t) a termék meghibásodási rátáját jelenti, azaz annak a valószínűségét, hogy egy termék a [t,t+dt] időintervallumban meghibásodik, tudva, hogy t időpontban nem hibásodott meg.
- λ(t) csökken A hibaarány idővel csökken, és ez általában megfelel a korai hibáknak. A belső hibás termékek gyorsan romlanak, míg más termékek sokkal tovább tartanak.
- λ(t) állandó A hibaarány nem függ az időtől. Ugyanannyira fennáll a kockázata annak, hogy egy termék t időpontban meghibásodik, függetlenül az élettartamától. Ezek belső hibák. Ez az a hibatípus, amely gyakran előfordul az elektronikai termékekben.
- λ(t) növekszik A meghibásodási arány idővel növekszik. A termék élettartamának növekedésével egyre nagyobb a kockázata annak, hogy meghibásodik. Ez a termék élettartamának végét jelenti.
MTTF (átlagos meghibásodásig eltelt idő)
Az MTTF, amelyet gyakrabban használnak a termékek megbízhatóságában, az első meghibásodásig eltelt átlagos idő.
MTBF (meghibásodások közötti átlagos idő)
Az MTBF (Mean Time Between Failures - átlagos meghibásodási idő) a két meghibásodás közötti időintervallum átlaga.
Weibull-törvény
Egy termék meghibásodási törvényének modellezéséhez többféle meghibásodástípust kell tudnia modellezni:
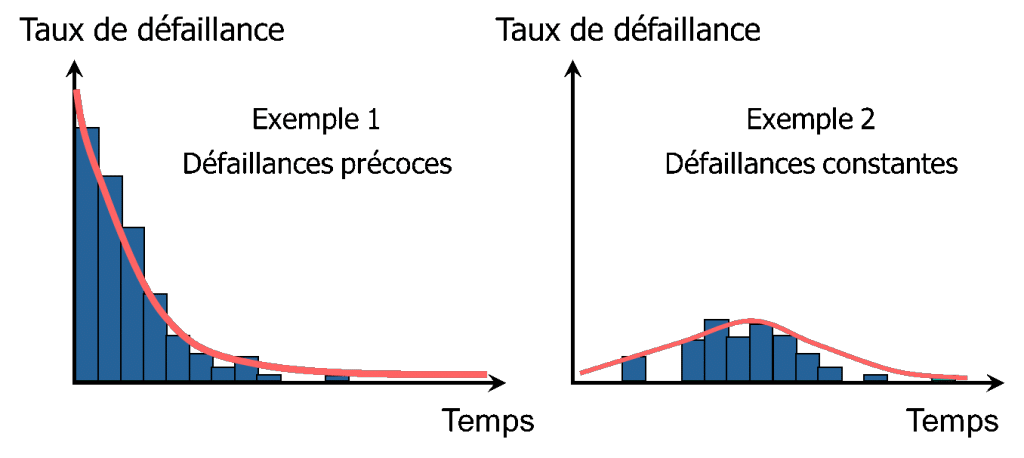
Emiatt elsősorban a Weibull-törvényt használják, mivel ez lehetővé teszi az alak nagyfokú változékonyságát.
Nagyfokú rugalmasságának köszönhetően a Weibull-törvény számos hibatípus viselkedésének modellezésére használható, mint például :
- Az alkatrészek szakítószilárdsága vagy a fémek fárasztásához szükséges erőkifejtés.
- Egy elektronikus alkatrész meghibásodási ideje
- A kültéren használt termékek, például autógumik meghibásodási ideje
- Olyan rendszerek, amelyek akkor hibásodnak meg, amikor a rendszer leggyengébb eleme meghibásodik.
A Weibull-törvény ugyanannak az alkatrésznek a különböző élethelyzetek viselkedésének modellezésére is használható.
A Weibull eloszlás függvénye a következő :
R\left( t \right)=e-\left( \frac{t-\delta}{\phi} \right)^{\beta}
3 paramétere van:
- \bétaalaki paraméter
- θ: skálázási paraméter
- \deltakésleltetési paraméter
βalaki paraméter
Ez lehetővé teszi, hogy a törvény alakját úgy igazítsuk ki, hogy az a lehető legközelebb álljon a megfigyelt meghibásodási arányhoz:
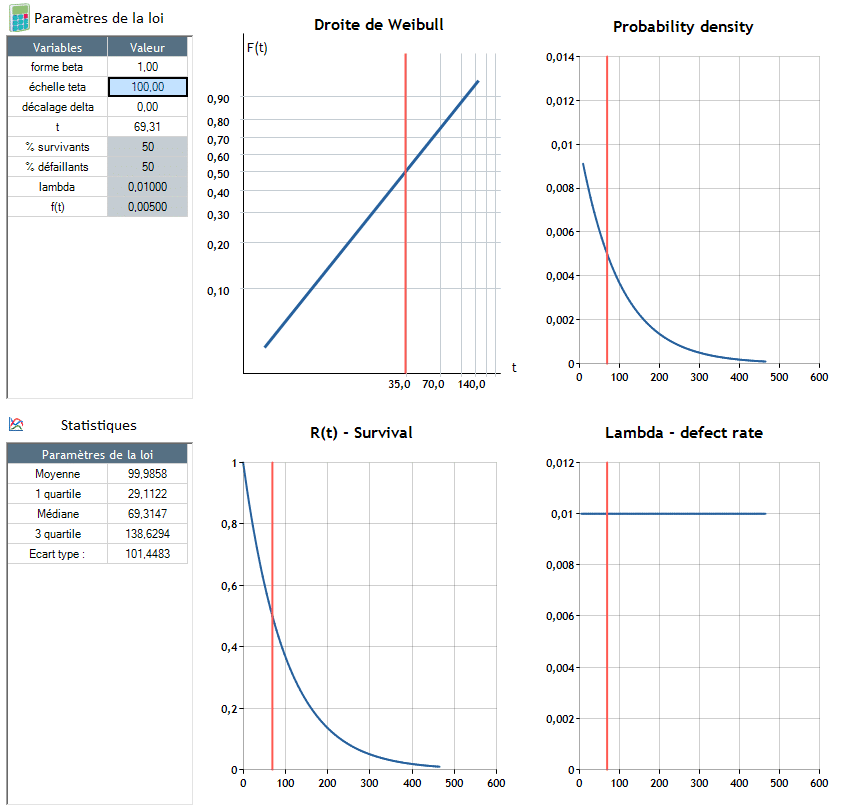
β=1: A meghibásodási arány állandó (λ állandó)
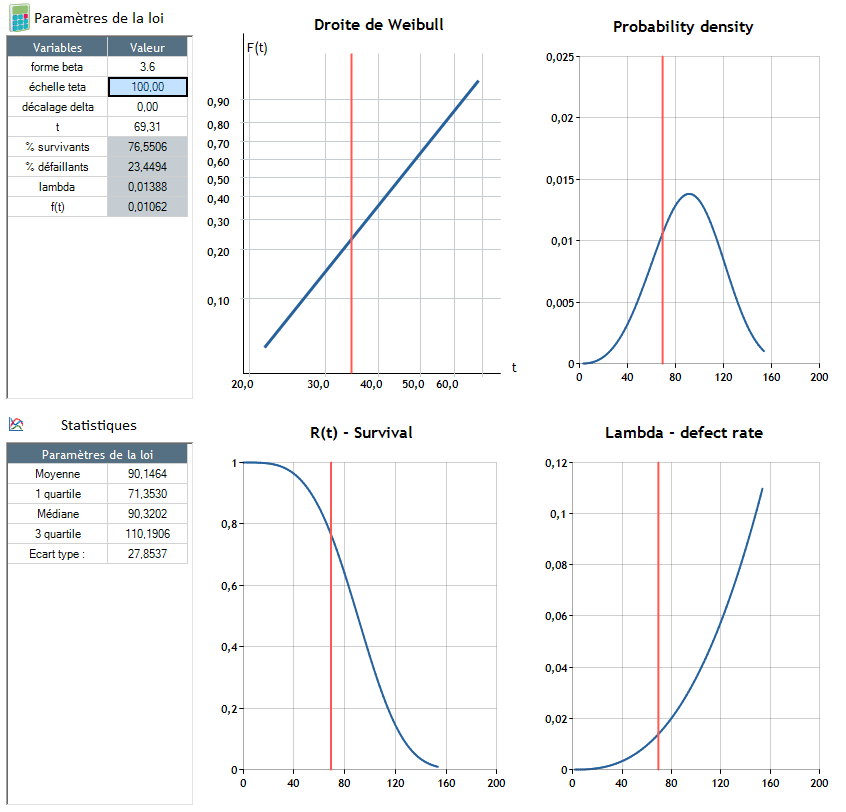
β>1: A meghibásodási arány az idő múlásával növekszik (λ növekszik - a termék élettartamának vége)
θ: skálázási paraméter
A θ paramétert arra használjuk, hogy az eloszlási törvény skáláját a megfigyelt probléma skálájához igazítsuk, például :
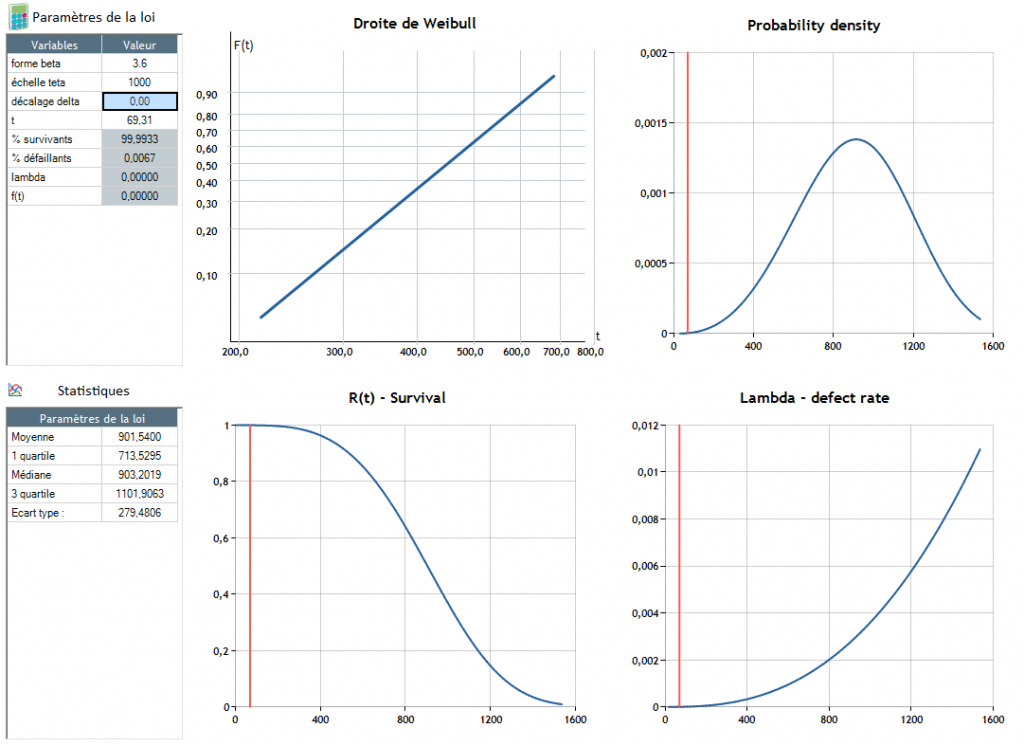
A meghibásodás t = 90,4 körül következik be
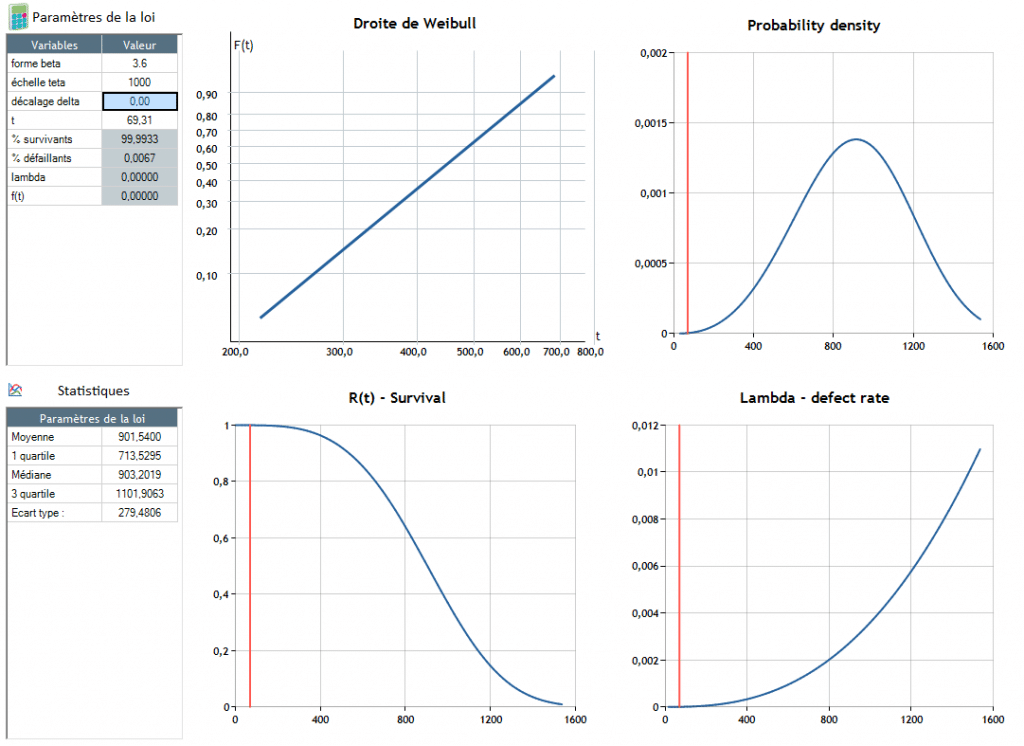
A meghibásodás t = 904 körül következik be
δkésleltetési paraméter
Az eloszlási törvény eltolható a δ paraméterrel
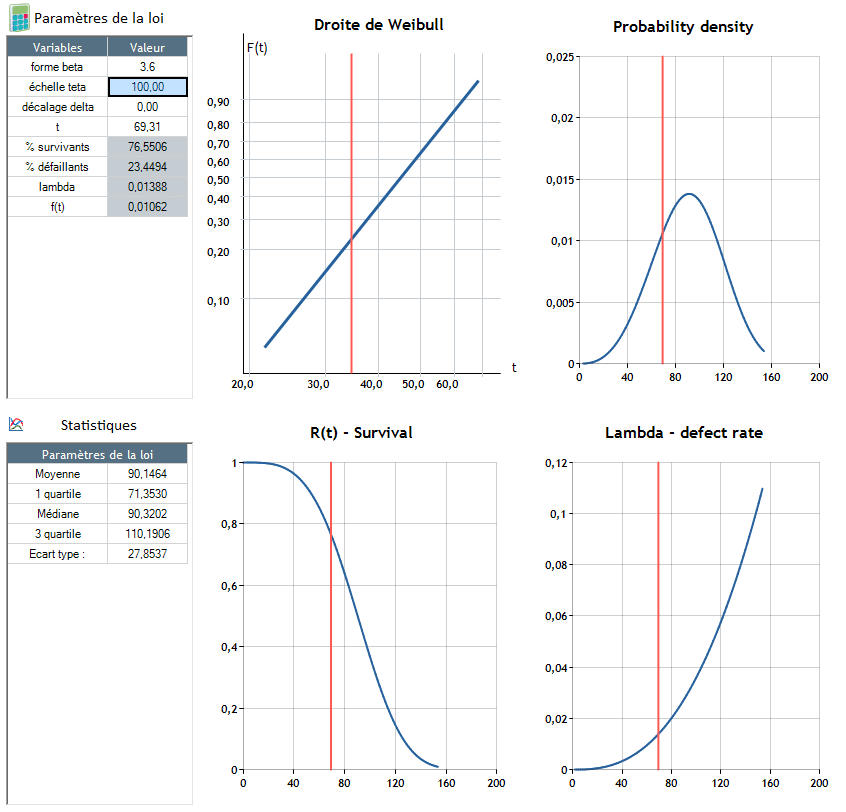
Β = 3,6 - θ = 100, δ = 0
A meghibásodás t = 90,4 körül következik be
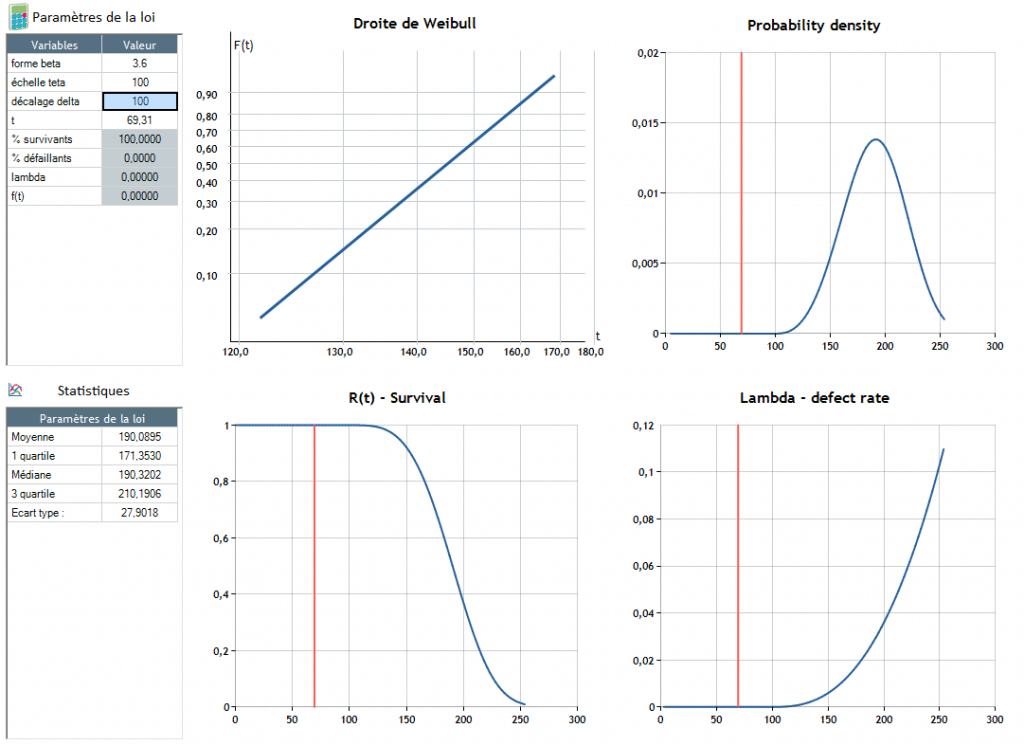
Β = 3,6 - θ = 100, δ = 100
A meghibásodás t = 190,4 körül következik be