La garanzia R&R viene utilizzata per qualificare un processo di misura. Ciò significa verificare che la variabilità del processo di misura sia compatibile con la variabilità della grandezza da misurare.
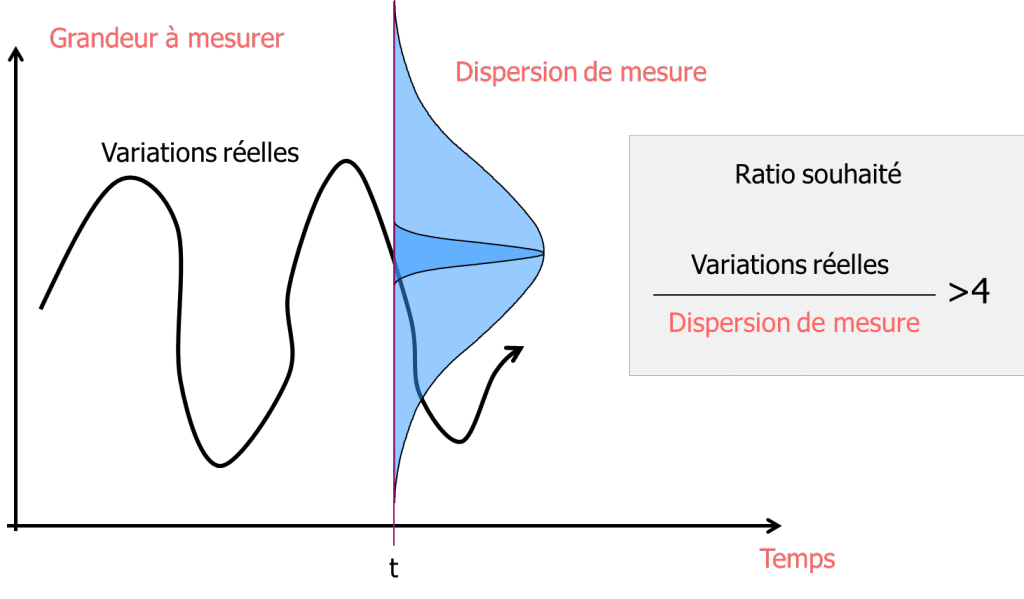
Si ritiene necessario un rapporto di 4 tra la variabilità dei pezzi e la variabilità della misura. Questo rapporto è espresso come Cpc di produzione:
\text{Cpc production}=\frac{text{dispersione di produzione}}{text{dispersione di misura}}
Il Cpc di produzione dipende quindi dalla dispersione dei pezzi. Tuttavia, quando vogliamo caratterizzare uno strumento di misura, vorremmo che questa caratterizzazione fosse indipendente dalla variabilità della produzione. Introdurremo quindi un nuovo tipo di variabile, che ci permetterà di caratterizzare lo strumento di misura non in termini di dispersione dei pezzi, ma in termini di intervallo di tolleranza dei pezzi.
Allo stesso modo in cui si calcola la capacità, si caratterizza lo strumento di misura:
- O da Cpc (Control Process Capability):
\text{Cpc}=\frac{{testo{intervallo di tolleranza}}{{testo{dispersione della misura}}> 4
- GRR% (Ripetibilità e riproducibilità):
{\text{GRR}=\frac{{{dispersione della misura}}{{text{intervallo di tolleranza}}<{text{0,3}}
Come si può vedere, i due indicatori rappresentano la stessa cosa e abbiamo la relazione :
\text{GRR}=\frac{\text{1}}{\text{Cpc}}
Ecco le regole generalmente accettate:
| Cpc | GRR% | |
|---|---|---|
| Inaccettabile | <3 | >30% |
| Processo di limitazione | >3 e < 4 | 20% |
| Accettabile | >4 | <20% |
| Eccellente | >8 | <10% |
Calcolo della dispersione di uno strumento di misura
Per calcolare la dispersione di un processo di misurazione, si utilizza un test di ripetibilità e riproducibilità.
Il test di ripetibilità e riproducibilità mira a caratterizzare la dispersione complessiva del processo di misurazione, separando ciò che è ripetibilità (cioè la dispersione della ripetizione della misura) da ciò che è riproducibilità (cioè una differenza tra diversi operatori).
Per eseguire questo test è necessario :
Test standard: 3 operatori misurano ciascuno 10 parti per 3 volte.
Test rapido: 3 operatori misurano 10 parti una volta ciascuno (questo test non separa la ripetibilità e la riproducibilità)
Una volta effettuate le misure, esistono due metodi per calcolare la dispersione del mezzo di misura:
Metodo ANAVAR : Un metodo più accurato, che calcola la ripetibilità e la riproducibilità e rileva l'eventuale presenza di interazioni tra pezzi e operatori.
Metodo RANGE : Un metodo più approssimativo, facile da calcolare con un foglio Excel, ma che non rileva alcuna interazione parte/operatore.
Si consiglia di mantenere il metodo di calcolo ANAVAR, in quanto è il più accurato.
Metodo della gamma
Il metodo della gamma è particolarmente utilizzato nell'industria perché i suoi calcoli possono essere facilmente eseguiti a mano.
Questo metodo può essere utilizzato per calcolare la ripetibilità e la riproducibilità del processo di misura. Tuttavia, non consente di calcolare l'interazione, il che ne limita la portata. I calcoli di questo metodo si basano sul calcolo della deviazione standard intra-campione rispetto agli intervalli.
Il principio di calcolo è il seguente:
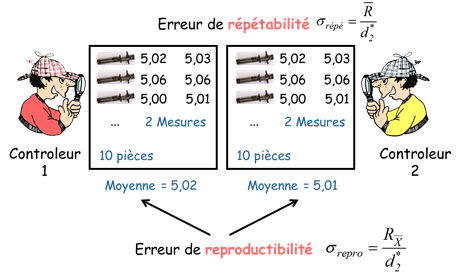
Tutte le misure di ciascun pezzo effettuate da ciascun operatore sono considerate un campione. In questo modo, la variabilità intra-campione rappresenta la ripetibilità del processo di misura, calcolata da :
\sigma_{repetablity}=\frac{\overline{R}}{d_{2}^{*}}
Consideriamo quindi le medie delle misure di ciascun operatore come un campione. In questo modo è possibile calcolare la riproducibilità del processo di misurazione mediante :
\sigma_{operator}=\frac{R_{\overline{X}}}{d_{2}^{*}}
Metodo ANAVAR
La Metodo ANAVAR è più complesso:
Per calcolare il GRR e il Cpc con il metodo ANAVAR, utilizziamo il test di Fisher:
| Fonti di variabilità | Somma dei quadrati | Grado di libertà | Quadrato medio | Statistica F |
|---|---|---|---|---|
| Operatore | SSA | a-1 | \text{MSA}=\frac{\text{SSA}}{\text{a-1}} | \text{F}=\frac{\text{MSA}}{\text{MSE}} |
| Parti di ricambio | SSB | b-1 | \text{MSB}=\frac{\text{SSB}}{\text{b-1}} | \text{F}=\frac{\text{MSB}}{\text{MSE}} |
| Interazione (operatore/parte) | SSAB | (a-1)(b-1) | \text{MSAB}=\frac{\text{SSAB}}{\text{(a-1)(b-1)}} | \text{F}=\frac{\text{MSAB}}{\text{MSE}} |
| Strumento | SSE | ab(n-1) | \text{MSE}=\frac{\text{SSE}}{\text{ab(n-1)}} | |
| Totale | TSS | N-1 |
con:
- a = numero di operatori
- b = numero di pezzi
- n = numero di ripetizioni
- N = numero totale di misure = abn
\text{SSA}=\sum^{a}{\frac{Y_{i}^{2}}{\text{bn}}}-\frac{Y_{**}^{2}}{N}
\text{SSB}=\sum^{b}{\frac{Y_{i}^{2}}{\text{an}}}-\frac{Y_{**}^{2}}{N}
\text{SSAB}=\sum^{a}\sum^{b}{\frac{Y_{ij}^{2}}{n}}-\frac{Y_{**}^{2}}{N}-\text{SSA}-\text{SSB}
\text{TSS}=\sum^{a}\sum^{b}\sum^{n}Y_{ijk}^{2}-\frac{Y_{**}^{2}}{N}
\text{SSE}=\text{TSS}-\text{SSA}-\text{SSB}-\text{SSAB}
La ripetibilità del processo di misurazione è data da :
\text{Répétabilité}=5.15\sqrt{\text{MSE}}
La riproducibilità del processo di misurazione è data da :
\text{Reproductibilité}=5.15\sqrt{\frac{\text{MSA}-\text{MSAB}}{\text{bn}}}
L'interazione è data da :
\text{Intéraction}=5.15\sqrt{\frac{\text{MSAB}-\text{MSE}}{\text{n}}}
La variabilità del processo di misurazione è data da
\text{Dispersione}=5,15\sqrt{text{Ripetibilità}^2+text{Riproducibilità}^2+text{Interpretazione}^2}
Infine, calcoliamo :
\text{GRR}=frac{Dispersione}{IT}
Questo metodo è quindi molto più complesso da implementare, ma consente di calcolare l'interazione come fonte di dispersione, cosa che non è possibile con il metodo RANGE. È quindi più accurato.