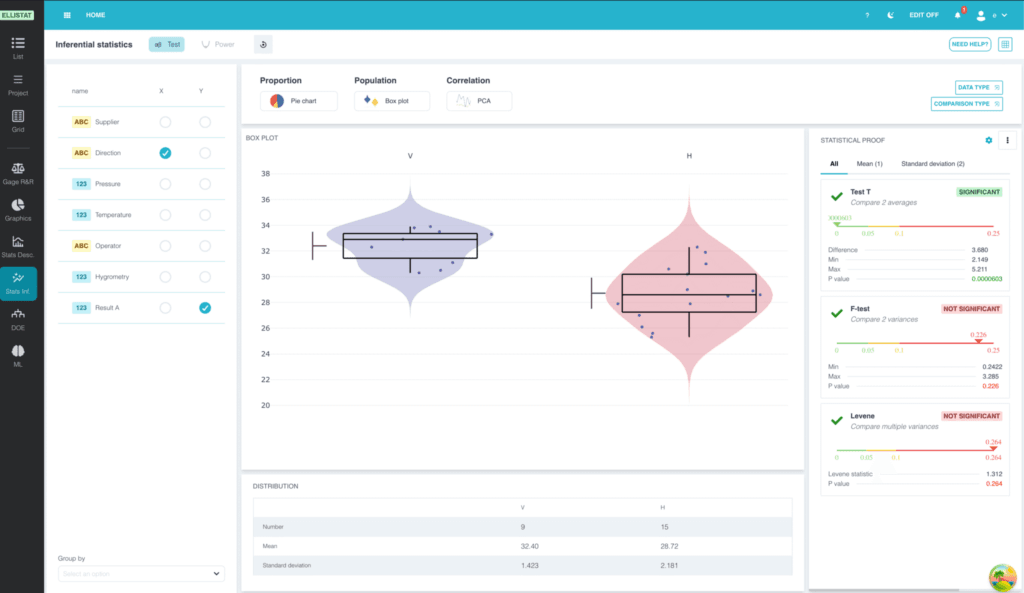
Prima di entrare nel dettaglio dei test parametrici e non parametrici, vediamo come funziona un test statistico. Il Modulo di analisi dei dati Ellistat consente di eseguire questi test.
Un test statistico funziona come segue:
- Consideriamo un'ipotesi nulla in cui non vi è alcuna differenza tra i campioni.
- Si calcola la probabilità di cadere nella stessa configurazione ottenuta con i campioni osservati sotto l'ipotesi nulla. Questa probabilità è nota come "rischio alfa" o "valore p".
- Se il rischio alfa è < 5%, si ritiene troppo improbabile ottenere una tale configurazione sotto l'ipotesi nulla. Si rifiuta quindi l'ipotesi nulla e si ritiene che la differenza tra i campioni sia significativa. Per questo motivo, tutti i risultati dei test statistici proposti da Ellistat saranno associati a un valore di rischio alfa con la seguente scala:
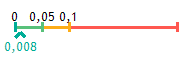
La cifra sotto la scala è pari al rischio alfa del test:
- Se il rischio alfa è < 0,01, la differenza sarà considerata altamente significativa<.
- Se il rischio alfa è < 0,05, la differenza è considerata significativa.
- Se il rischio alfa è inferiore a 0,1, la differenza è considerata borderline (non si può dire che ci sia una differenza significativa, ma l'ipotesi è interessante).
- Se il rischio alfa è > 0,1, la differenza sarà considerata non significativa.
Esempio
Per illustrare il funzionamento di un test statistico, prendiamo il seguente esempio.
Supponiamo di voler rilevare il fatto che una moneta viene lanciata lanciando testa o croce. Supponiamo che la moneta cada sempre su croce.
Lancio n°1
Dopo il primo lancio, la moneta cade su croce. Possiamo dedurre da questo che la moneta è stata ribaltata?
A prima vista, sarebbe piuttosto rischioso scommettere che la moneta è un pipedding, dato che potrebbe benissimo essere successo con una moneta standard.
In questo caso, l'ipotesi nulla è: la moneta non è rovesciata, quindi ha una possibilità su due di uscire testa o croce. La probabilità che una moneta non rovesciata esca testa è 50%.
Di conseguenza, la probabilità di ottenere croce dopo il primo lancio di una moneta non lanciata è 50%, si dice che il rischio alfa del test è:Rischio alfa = 50%
In altre parole, c'è una probabilità di 50% di ottenere lo stesso risultato seguendo l'ipotesi nulla.
Lancio n°2
Dopo il secondo lancio, la moneta cade nuovamente su croce. Il rischio alfa diventa: Rischio alfa = 25%
Ma questo significa che il gioco è truccato?
Sorge quindi la domanda: a quale rischio alfa possiamo dire che la moneta è stata ribaltata?
Come regola generale, nell'industria il limite di rischio alfa è fissato a 5%.
In altre parole :
- Se il rischio alfa è inferiore a 5%, l'ipotesi nulla viene rifiutata e la moneta viene considerata ribaltata.
- Se il rischio alfa è > 5%, non si può dire che la moneta sia ribaltata. Tuttavia, questo non significa che la moneta non sia ribaltata, poiché ciò dipende dal numero di lanci effettuati.
Esempio continuato
Continuiamo con il nostro esempio:
-3th Lancio: la moneta cade su croce: rischio alfa = 12,5%
-4th Lancio: la moneta cade su croce: rischio alfa = 6,75%
-5th Lancio: la moneta cade su croce: rischio alfa = 3,375%
In questo caso, da 5th Possiamo quindi affermare che la moneta è ribaltata con un rischio inferiore a 5%.
Test parametrici e non parametrici
Quando si effettuano confronti tra popolazioni o si confronta una popolazione con un valore teorico, esistono due tipi principali di test: i test parametrici e i test non parametrici.
Test parametrici
I test parametrici partono dal presupposto che i dati a disposizione seguano una legge di distribuzione nota (generalmente la legge normale).
Per calcolare il rischio alfa del test statistico, è sufficiente calcolare la media e la deviazione standard del campione per accedere alla legge di distribuzione del campione.
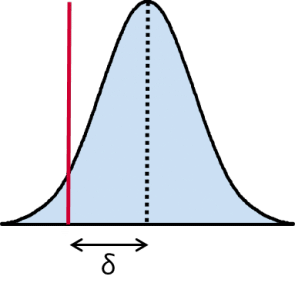
Con la legge di distribuzione perfettamente nota, il rischio alfa può essere calcolato sulla base dei calcoli teorici per la distribuzione gaussiana.
Questi test sono generalmente molto validi, ma richiedono che i dati seguano effettivamente la distribuzione ipotizzata. In particolare, sono molto sensibili ai valori anomali e non sono consigliati se vengono rilevati valori anomali.
Test non parametrici
I test non parametrici non fanno ipotesi sul tipo di legge di distribuzione dei dati. Si basano esclusivamente sulle proprietà numeriche dei campioni. Ecco un esempio di test non parametrico:
Vogliamo verificare che la mediana di una popolazione sia diversa da un valore teorico. Misuriamo 14 pezzi e otteniamo il seguente campione:

11 volte sullo stesso lato su 14
11 volte su 14, il risultato è inferiore alla mediana teorica. Se la mediana della popolazione è uguale al valore teorico, dovremmo avere 50% di monete sopra la mediana e 50% di monete sotto. Per determinare se la deviazione della mediana dalla mediana teorica è significativa, basta verificare se la frequenza di 11 volte su 14 è significativamente diversa da 50%.
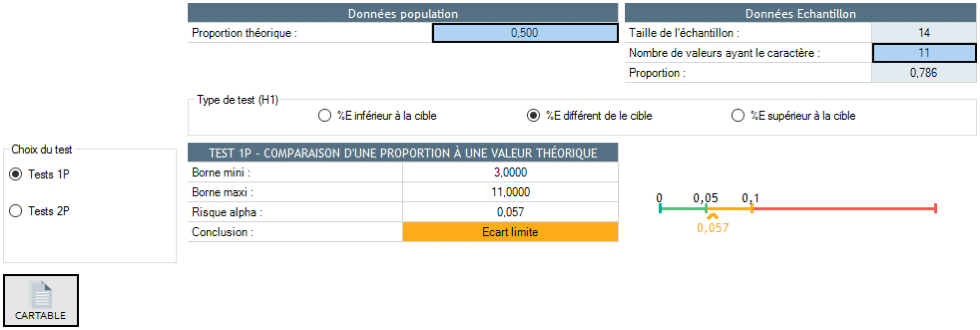
Questo divario è al limite.
Come nell'esempio precedente, i test non parametrici non hanno bisogno di assumere un particolare tipo di distribuzione per calcolare il rischio alfa del test. Sono molto eleganti e si basano su proprietà numeriche. Inoltre, non sono molto sensibili agli outlier e sono quindi consigliati in questo caso.