Parametric and non-parametric statistical tests

Before going into the details of parametric and non-parametric tests, let's look at how a statistical test works. The Ellistat Data Analysis module allows you to carry out these tests.

A statistical test works as follows:

We consider a null hypothesis in which there is no difference between the samples.
The probability of falling into the same configuration as that obtained with the samples observed under the null hypothesis is calculated. This probability is known as the "alpha risk" or "p-value".
If alpha risk < 5%, it is considered too unlikely to obtain such a configuration under the null hypothesis. We therefore reject the null hypothesis and consider that the difference between the samples is significant. For this reason, all the results of the statistical tests proposed by Ellistat will be associated with an alpha risk value with the following scale:

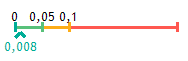
The figure below the scale is equal to the alpha risk of the test:

If alpha risk < 0.01, the difference will be considered highly significant<.
If alpha risk < 0.05, the difference is considered significant
If the alpha risk is less than 0.1, the difference is considered to be borderline (it cannot be said that there is a significant difference, but the hypothesis is interesting).
If alpha risk > 0.1, the difference will be considered insignificant

Example

To illustrate how a statistical test works, let's take the following example.

Suppose we want to detect the fact that a coin is tipped by flipping it heads or tails. We assume that the coin always lands on tails.

Throw n°1

After the first toss, the coin lands on tails. Can we deduce from this that the coin has been tipped?

On the face of it, it would be rather risky to bet that the coin is piped, as it could just as easily have happened with a standard coin.

In this case, the null hypothesis is: the coin is not tipped, so it has one chance in two of coming up heads or tails. The probability of an unpiped coin coming up heads is 50%.

As a result, the probability of getting tails after the first toss of an unpiped coin is 50%, so the alpha risk of the test is :

Alpha risk = 50%

In other words, there is a 50% chance of obtaining the same result by following the null hypothesis.

Throw n°2

After the second toss, the coin lands on tails again. The alpha risk becomes :

Alpha risk = 25%

Does this mean that the game has been rigged?

So the question arises: at what alpha risk can we say that the coin has been tipped?

As a general rule, in industry, the alpha risk limit is set at 5%.

In other words :

If the alpha risk is less than 5%, the null hypothesis is rejected and the coin is considered to be tipped.
If the alpha risk is > 5%, it cannot be said that the coin is tipped. However, this does not mean that the coin is not piped, as this depends on the number of throws made.

Example continued

Let's continue with our example:

3^th Toss: coin lands on tails: alpha risk = 12.5%4^th Toss: coin lands on tails: alpha risk = 6.75%5^th Toss: coin lands on tails: alpha risk = 3.375%

In this case, from 5^th We can therefore say that the coin is tipped with a risk of less than 5%.

Parametric vs. non-parametric tests

When making population comparisons or comparing a population with a theoretical value, there are two main types of test: parametric tests and non-parametric tests.

Parametric tests

Parametric tests work on the assumption that the data we have available follows a known type of distribution law (generally the normal law).

To calculate the alpha risk of the statistical test, simply calculate the mean and standard deviation of the sample in order to access the distribution law of the sample.

With the distribution law perfectly known, the alpha risk can be calculated on the basis of the theoretical calculations for the Gaussian distribution.

These tests are generally very fine, but they require the data to actually follow the assumed distribution. In particular, they are very sensitive to outliers and are not recommended if outliers are detected.

Non-parametric tests

Non-parametric tests make no assumptions about the type of distribution law of the data. They are based solely on the numerical properties of the samples. Here is an example of a non-parametric test:

We want to check that the median of a population is different from a theoretical value. We measure 14 pieces and obtain the following sample:

11 times on the same side out of 14

11 times out of 14, the result is below the theoretical median. If the median of the population is equal to the theoretical value, we should have 50% of coins above the median and 50% of coins below. To determine whether the deviation of the median from the theoretical median is significant, all we need to do is check whether the frequency of 11 times out of 14 is significantly different from 50%.

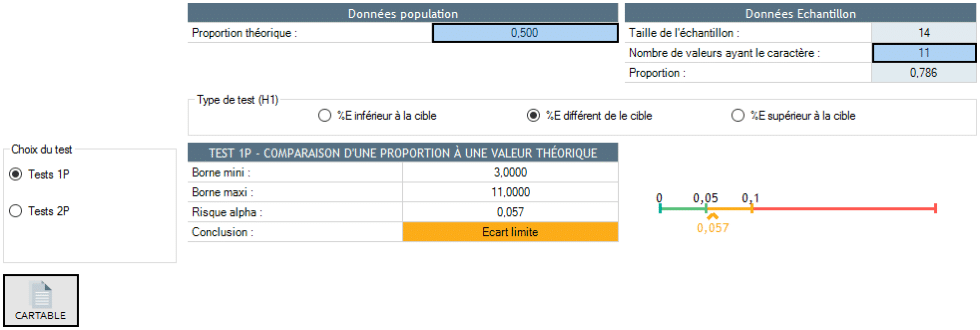
This gap is borderline.

As in the previous example, non-parametric tests do not need to assume a particular type of distribution in order to calculate the alpha risk of the test. They are very elegant and are based on numerical properties. What's more, they are not very sensitive to outliers and are therefore recommended in this case.

Here are the modules you can use to calculate these indicators:

Data Analysis

Statistics in 1 click. Use the power of statistics to find out what's behind your production data from the SPC, APC or IQC modules. Thanks to its machine learning algorithms, the Data Analysis module can be used to understand the origin of machine drift or to differentiate suppliers statistically.