Die Weibull-Verteilung ist die am häufigsten verwendete Methode zur Modellierung von Zuverlässigkeitsdaten. Das Data Analysis-Modul von Ellistat ermöglicht es Ihnen, diese Analysen ganz einfach durchzuführen.
Definitionen: Zuverlässigkeit, Weibull-Gesetz, Ausfall
Zuverlässigkeit:
Zuverlässigkeit ist die Fähigkeit einer Einheit, eine geforderte Funktion unter bestimmten Bedingungen für einen bestimmten Zeitraum zu erfüllen.
Ausfall:
Ein Ausfall ist das Ende der Fähigkeit eines Geräts, eine erwartete Funktion zu erfüllen. Er kann teilweise (Leistungsbeeinträchtigung) oder vollständig (Ende der Funktion) sein.
R(t): Wahrscheinlichkeit, dass eine Einheit E über den Zeitraum [0; t ] nicht ausfällt, unter der Annahme, dass sie zum Zeitpunkt t = 0 nicht ausfällt.
F(t): F(t) ist die kumulierte Funktion der Ausfälle è F(t) = 1 - R(t)
Wahrscheinlichkeitsdichte : f(t) stellt die Ausfallrate eines Produkts dar, d. h. die Wahrscheinlichkeit, dass ein Produkt im Zeitintervall [t,t+dt] ausfällt.
????(????)=Anzahl der deˊfaillierenden eˊlemente über eine ZeitΔ????Anzahl der getesteten eˊleˊmenteˊs.f(t)=Anzahl der getesteten eˊleˊElementeˊAnzahl der deˊfaillierenden eˊlemente im Laufe einer ZeitΔ.t
λ(t) oder Ausfallrate : λ(t) steht für die Ausfallrate eines Produkts, d. h. die Wahrscheinlichkeit, dass ein Produkt im Zeitintervall [t,t+dt] ausfällt, wenn man weiß, dass es zum Zeitpunkt t nicht ausgefallen war
????(????)=Anzahl der eˊleˊmente mitˊFehlern während einer ZeitΔ????Anzahl der eˊlemente mitˊFehlern, die sich noch im Test befinden.λ(t)=Anzahl der noch im Test befindlichen eˊleˊFailing-ElementeˊAnzahl der eˊleˊFailing-Elemente im Laufe einer ZeitΔ.t
- λ(t) sinkt : Die Fehlerquote nimmt mit der Zeit ab, dies entspricht in der Regel Jugendfehlern. Produkte mit intrinsischen Fehlern verschlechtern sich schnell, während andere Produkte viel länger halten.
- λ(t) konstant : Die Ausfallrate ist nicht zeitabhängig. Die Wahrscheinlichkeit, dass ein Produkt zum Zeitpunkt t ausfällt, ist unabhängig von seiner Lebensdauer gleich groß. Hierbei handelt es sich um intrinsische Ausfälle. Dies ist die Art von Ausfällen, die man häufig bei elektronischen Produkten findet.
- λ(t) nimmt zu : Die Ausfallrate steigt mit der Zeit. Es besteht ein immer größeres Risiko, dass ein Produkt ausfällt, wenn seine Lebensdauer zunimmt. Es handelt sich dabei um das Ende der Lebensdauer des Produkts.
MTTF (Mean Time To Failure)
Die eher in der Produktzuverlässigkeit verwendete MTTF ist die durchschnittliche Zeit bis zum Auftreten des ersten Ausfalls.
MTBF (Mean Time Between Failure - mittlere Zeit zwischen Ausfällen)
Die MTBF (Mean Time Between Failure) ist der Durchschnitt der Zeitintervalle zwischen dem Auftreten von Ausfällen.
Weibull-Gesetz
Um das Ausfallgesetz eines Produkts zu modellieren, muss man in der Lage sein, mehrere Ausfallarten zu modellieren:
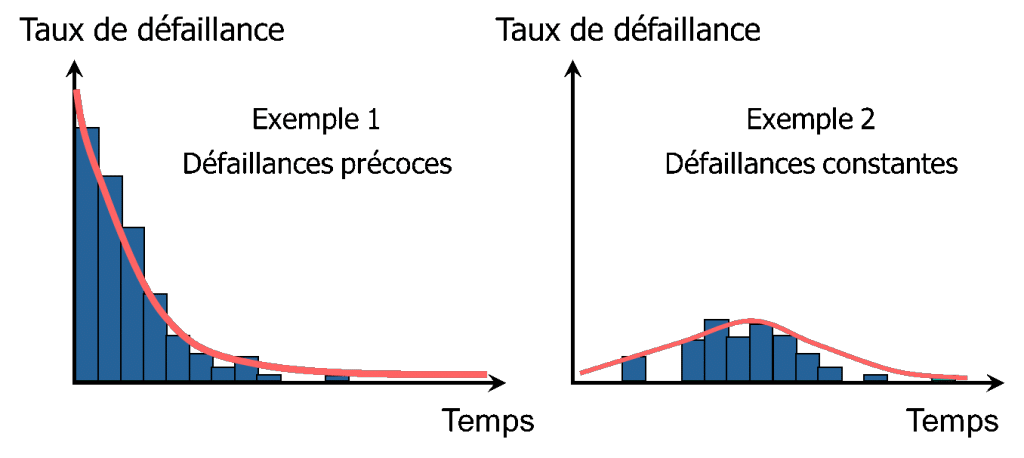
Es ist also eine große Flexibilität in den Formen erforderlich. Deshalb ist das hauptsächlich verwendete Gesetz das Weibull-Gesetz, da es eine große Variabilität in den Formen ermöglicht.
Aufgrund seiner großen Flexibilität ermöglicht das Weibullsche Gesetz die Modellierung des Verhaltens vieler Arten von Ausfällen wie :
- Die Bruchfestigkeit von Komponenten oder der Aufwand, der erforderlich ist, um Metalle zu ermüden
- Die Ausfallzeit eines elektronischen Bauteils
- Die Ausfallzeit für Artikel, die im Freien verwendet werden, wie z. B. Autoreifen
- Systeme, die versagen, wenn die schwächste Komponente im System einen Ausfall hat
Das Weibullsche Gesetz ermöglicht es auch, das Verhalten verschiedener Lebenssituationen einer Komponente zu modellieren
Die Funktion der Weibull-Verteilung lautet wie folgt:
Rleft( t \c&H30D3F4&} =e-left( \c&H30D3F4&} ^{beta})
Sie besteht aus drei Parametern:
- ????: Formparameter
- θ: Skalierungsparameter
- ????: Verzögerungseinstellung
β: Formparameter
Er ermöglicht es, die Form des Gesetzes so anzupassen, dass sie der festgestellten Ausfallrate am nächsten kommt:
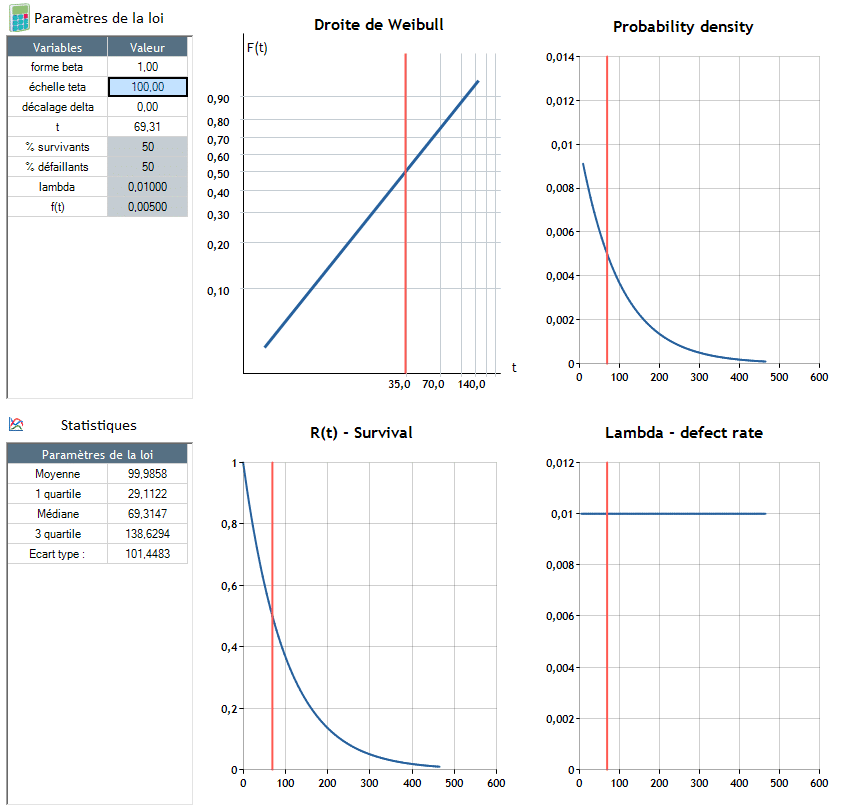
β=1: Die Ausfallrate ist konstant (λ konstant)
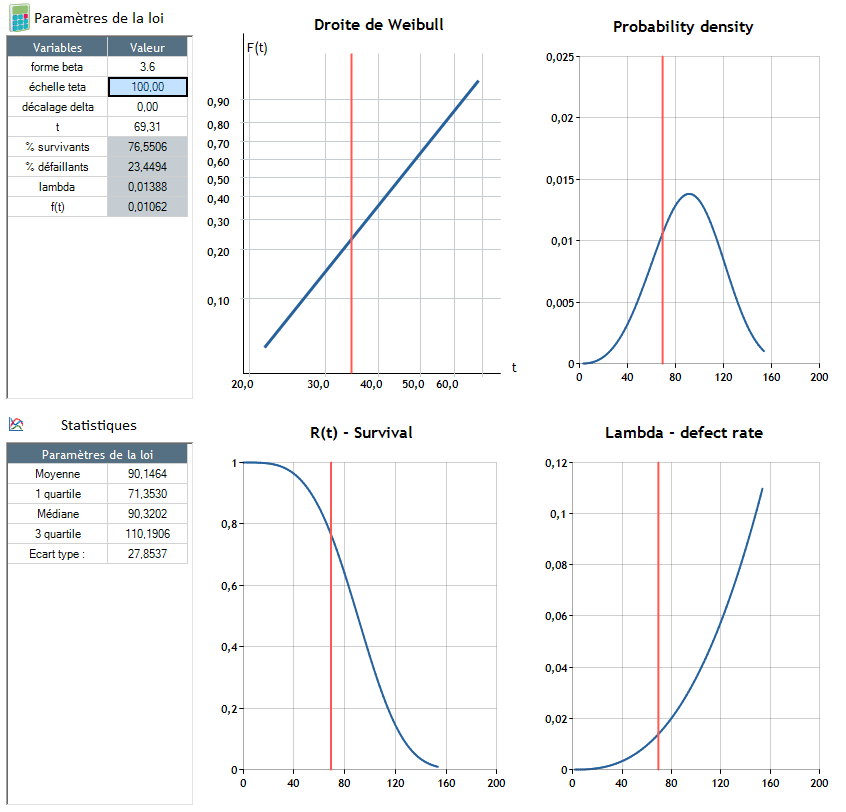
β>1: Die Ausfallrate steigt mit der Zeit (λ erhöht - Ende des Lebens eines Produkts)
θ: Skalierungseinstellung
Mit dem Parameter θ kann die Skalierung des Verteilungsgesetzes an die Skalierung des festgestellten Problems angepasst werden, z. B. :
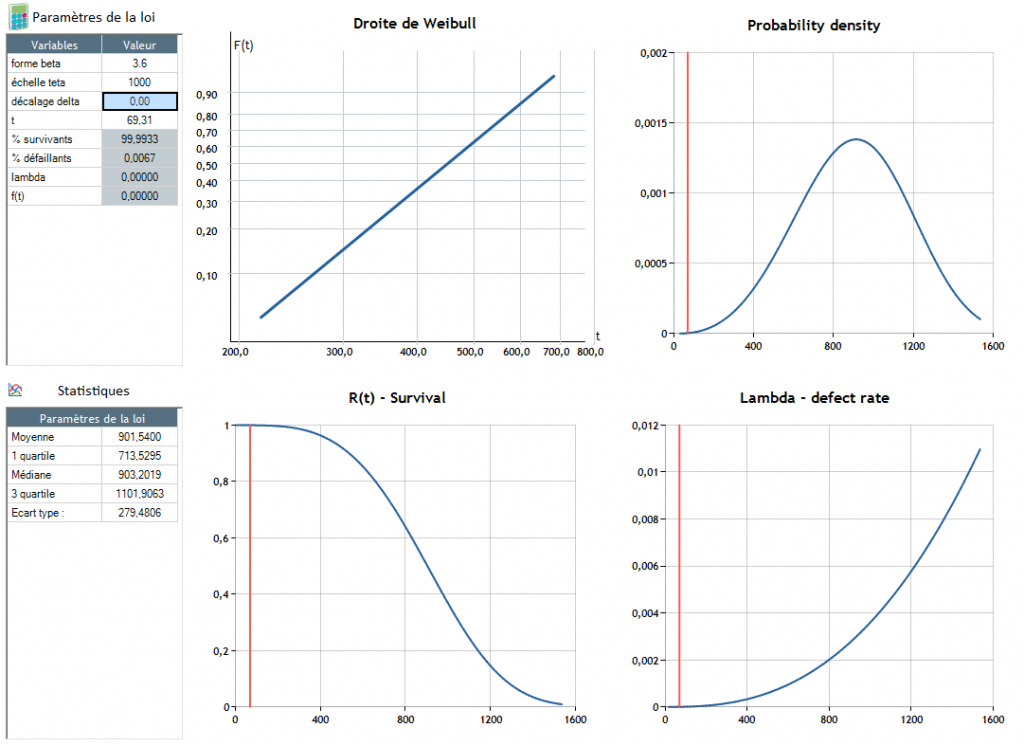
Der Ausfall tritt bei t = 90.4 auf.
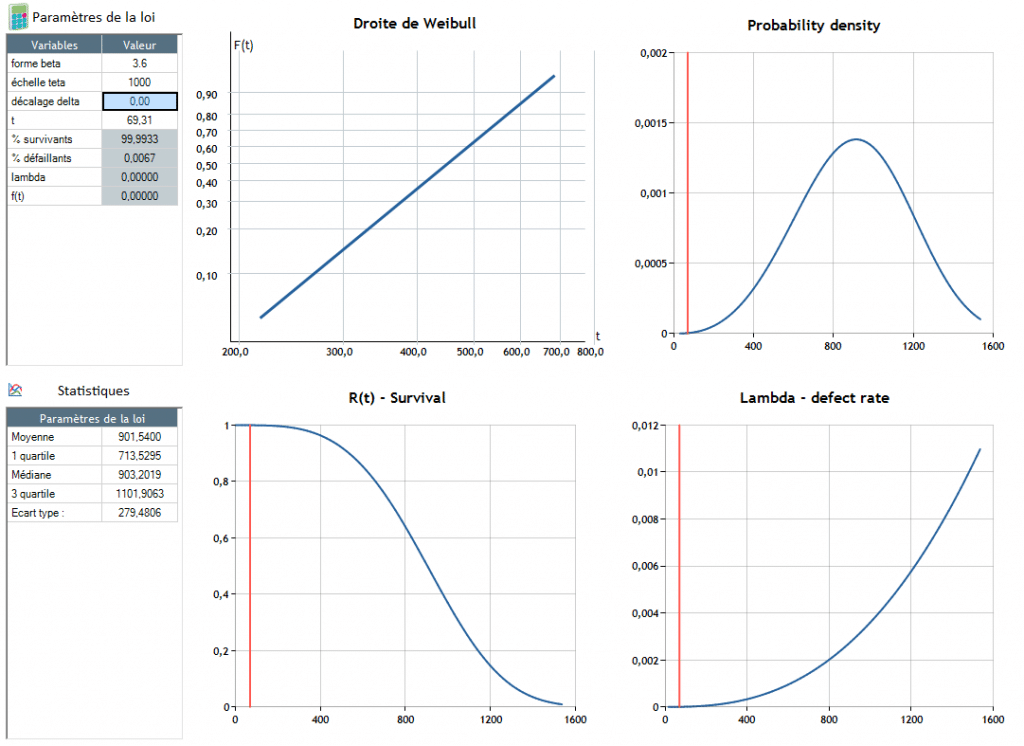
Der Ausfall tritt bei t = 904 auf.
δ: Verzögerungsparameter
Mit dem Parameter δ kann die Verteilungsgesetzlichkeit um einen Parameter δ verschoben werden.
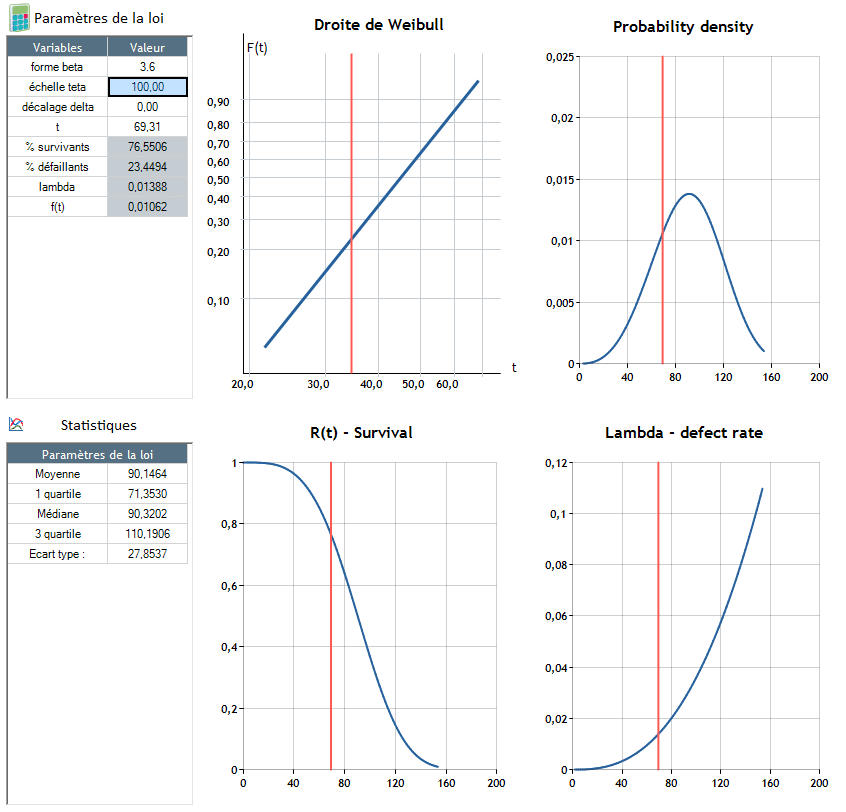
Β = 3,6 - θ = 100, δ = 0
Der Ausfall tritt bei t = 90.4 auf.
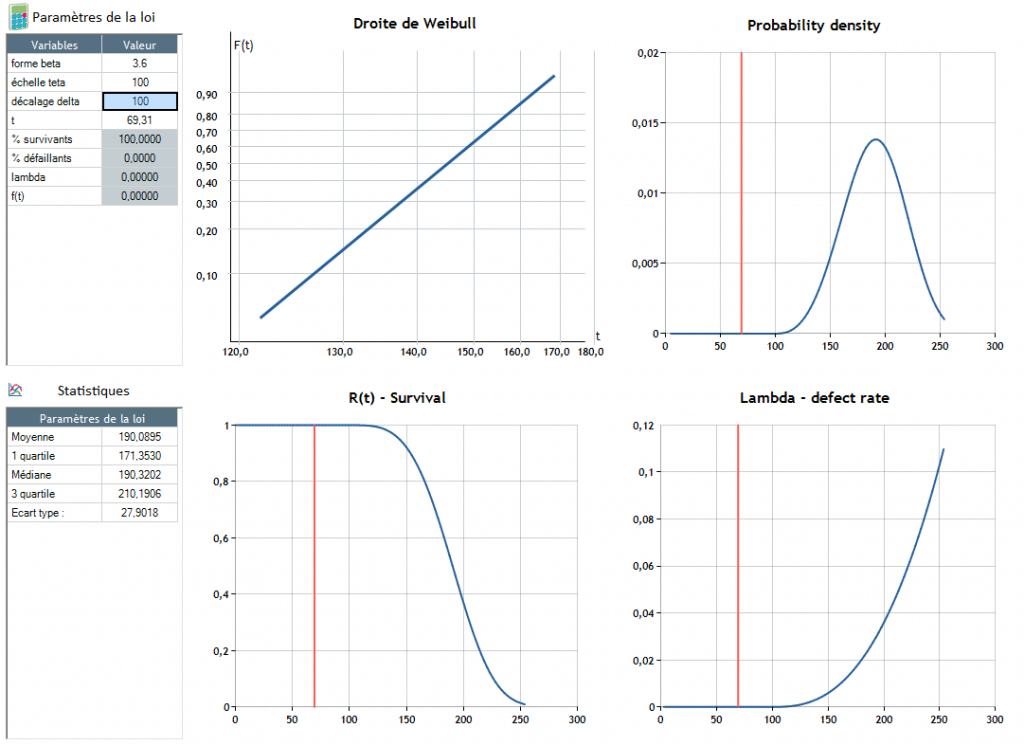
Β = 3,6 - θ = 100, δ = 100
Der Ausfall tritt bei t = 190.4 auf.
