La loi de Weibull est la plus souvent utilisée pour modéliser des données de fiabilité. Le module Data Analysis d’Ellistat vous permet de réaliser ces analyses en toute simplicité.
Définitions : Fiabilité, Loi de Weibull, Défaillance
Fiabilité:
La fiabilité est l’aptitude d’une entité à accomplir une fonction requise, dans des conditions données, pendant un intervalle de temps donné.
Défaillance:
La défaillance est la fin de l’aptitude d’un dispositif à accomplir une fonction que l’on attendait. Elle peut être partielle (altération des performances) ou totale (fin de la fonction).
R(t): Probabilité qu’une entité E soit non défaillante sur la durée [0 ; t ], en supposant qu’elle n’est pas défaillante à l’instant t = 0
F(t): F(t) est la fonction cumulée des défaillances è F(t) = 1 – R(t)
Densité de probabilité : f(t) représente le taux de défaillance d’un produit, c’est-à-dire la probabilité qu’un produit soit défaillant sur l’intervalle de temps [t,t+dt]
????(????)=nombre d’eˊlements deˊfaillants au cours d’un tempsΔ????nombre d’eˊleˊments testeˊsf(t)=nombre d’eˊleˊments testeˊsnombre d’eˊlements deˊfaillants au cours d’un tempsΔt
λ(t) ou taux de défaillance : λ(t) représente le taux de défaillance d’un produit, c’est-à-dire la probabilité qu’un produit soit défaillant sur l’intervalle de temps [t,t+dt] sachant qu’il n’était pas défaillant à l’instant t
????(????)=nombre d’eˊleˊments deˊfaillant au cours d’un tempsΔ????nombre d’eˊlements deˊfaillants encore en testλ(t)=nombre d’eˊlements deˊfaillants encore en testnombre d’eˊleˊments deˊfaillant au cours d’un tempsΔt
- λ(t) diminue : le taux de défaut diminue avec le temps, cela correspond en général à des défauts de jeunesse. Les produits avec des défaillances intrinsèques s’altèrent rapidement alors que les autres produits durent beaucoup plus longtemps.
- λ(t) constant : le taux de défaillance ne dépend pas du temps. Il y a autant de risque qu’un produit soit défaillant à l’instant t quelle que soit sa durée de vie. Il s’agit des défaillances intrinsèques. C’est le type de défaillance que l’on retrouve souvent sur des produits électroniques.
- λ(t) augmente : le taux de défaillance augmente avec le temps. Il y a de plus en plus de risque qu’un produit soit défaillant lorsque sa durée de vie augmente. Il s’agit de la fin de vie du produit.
MTTF (Mean Time To Failure)
Le MTTF plutôt utilisé en Fiabilité des produits est la moyenne des temps avant l’apparition de la première défaillance.
MTBF (Mean Time Between Failure)
Le MTBF (Temps moyen de bon fonctionnement) est la moyenne des intervalles de temps entre deux apparitions de défaillances.
Loi de Weibull
Pour modéliser la loi de défaillance d’un produit, il faut être capable de modéliser de multiple types de défaillance :
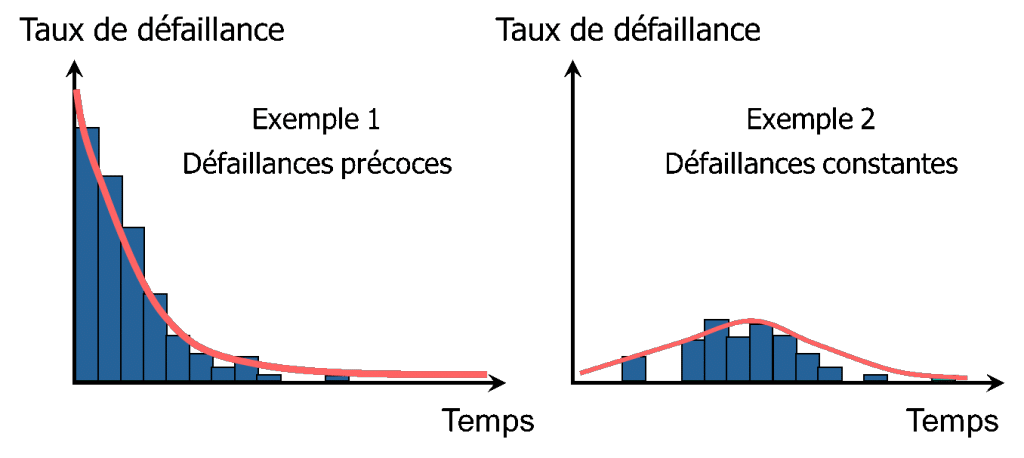
Il faut ainsi une grande flexibilité dans les formes, pour cela, la loi principalement utilisée est la loi de Weibull, car elle permet une grande variabilité de forme.
Grâce à sa grande flexibilité, la loi de Weibull permet de modéliser le comportement de nombreux types de défaillances telles que :
- La résistance à la rupture des composants ou l’effort requis pour fatiguer des métaux
- Le temps de défaillance d’un composant électronique
- Le temps de défaillance pour des articles utilisés en extérieur tels que les pneumatiques automobiles
- Les systèmes qui faillissent lorsque le composant le plus faible dans le système a une défaillance
La loi de Weibull permet également de modéliser le comportement de différentes situations de vie d’un même composant
La fonction de la loi de Weibull est la suivante :
R\left( t \right)=e-\left( \frac{t-\delta}{\phi} \right)^{\beta}
Elle comporte 3 paramètres :
- ????: paramètre de forme
- θ : paramètre d’échelle
- ????: paramètre de retard
β: paramètre de forme
Il permet d’adapter la forme de la loi pour être le plus proche du taux de défaillance constaté :
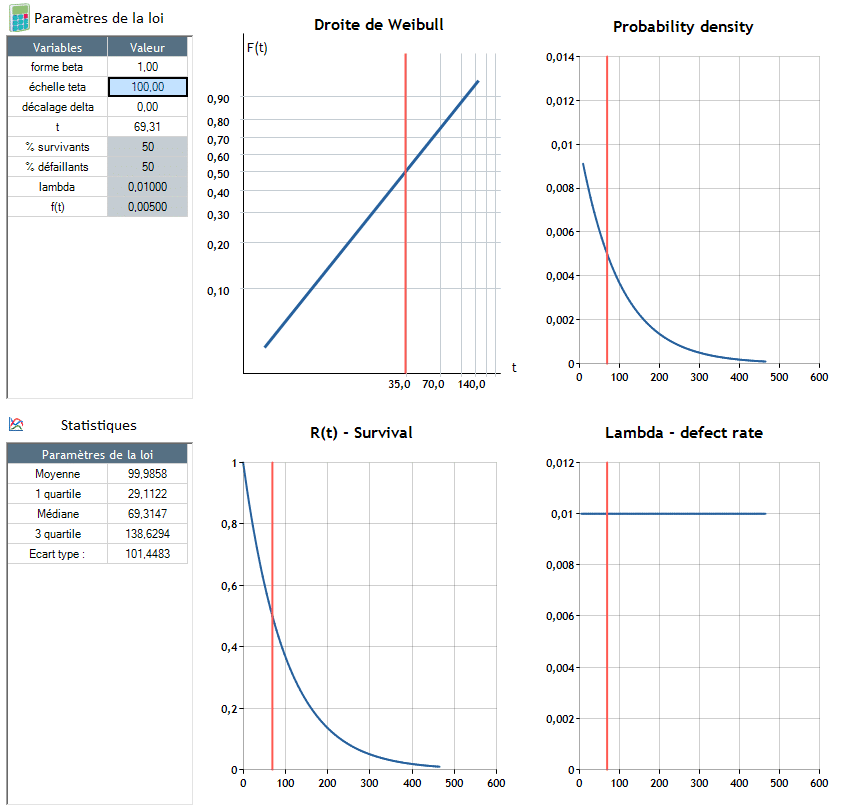
β=1 : Le taux de défaillance est constant (λ constant)
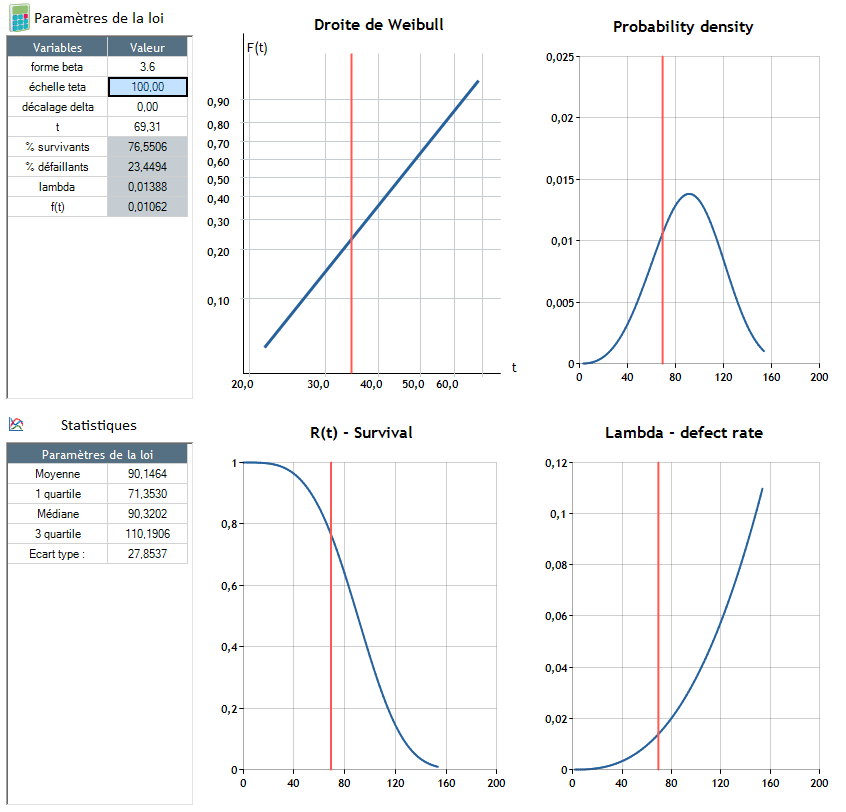
β>1 : Le taux de défaillance augmente avec le temps (λ augmente – fin de vie d’un produit)
θ: paramètre d’échelle
Le paramètre θ permet d’ajuster l’échelle de la loi de distribution à l’échelle du problème constaté, par exemple :
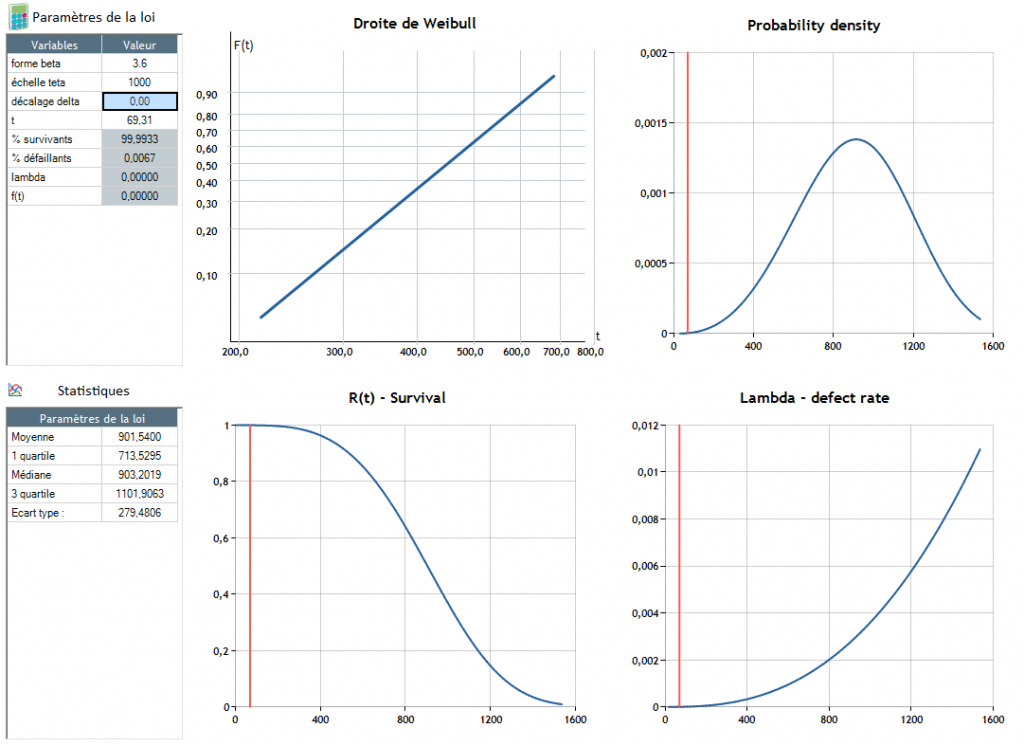
La défaillance apparait autour de t = 90.4
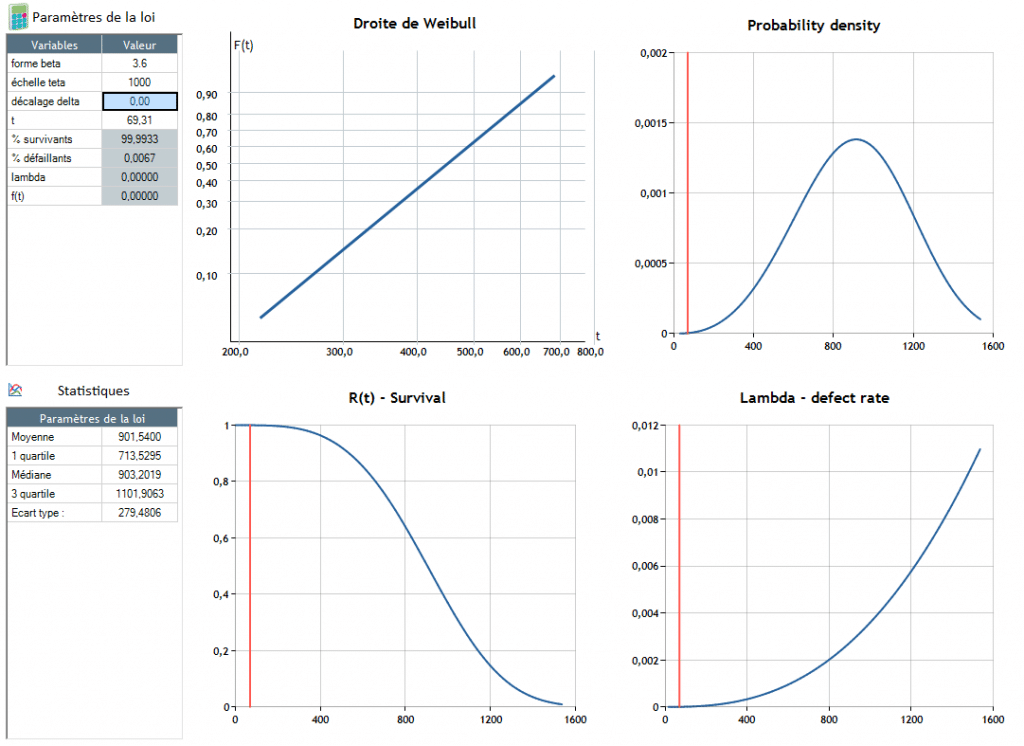
La défaillance apparait autour de t = 904
δ: paramètre de retard
Le paramètre δ permet de déplacer la loi de distribution d’un paramètre δ
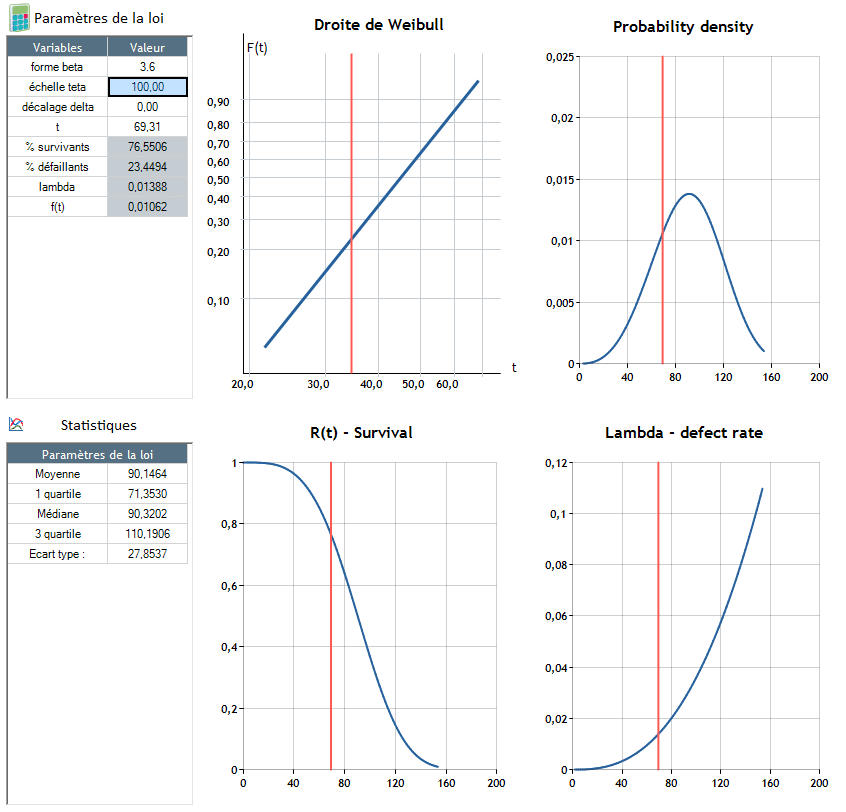
Β = 3,6 – θ = 100, δ = 0
La défaillance apparait autour de t = 90.4
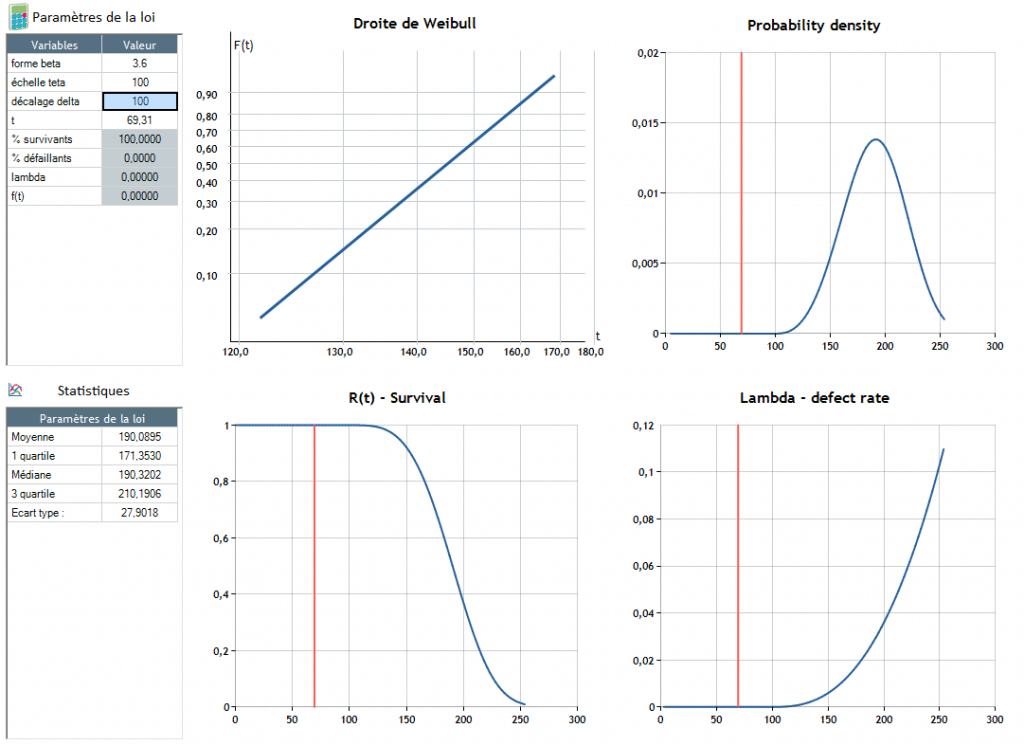
Β = 3,6 – θ = 100, δ = 100
La défaillance apparait autour de t = 190.4
