Ellistat Data Analysis propose le sous-menu Corrélation, qui contient plusieurs outils statistiques. Ces outils permettent de réaliser des études de corrélation de plusieurs réponses dans un jeu de données. Ou de réduire la dimension d’un jeu de données ou surveiller des processus avec plusieurs variables simultanément .
Dans les exemples ci-dessous on présente les outils :
- Matrice de corrélation
- ACP
- Carte T²
Le jeu de donnée utilisé dans ces exemple se trouve dans la page suivante
Independent Data 🇺🇸/ Données indépendantes🇫🇷
Exemple 1 : Trouver la corrélation entre plusieurs réponses Y, avec la matrice de corrélation
La matrice de corrélation est un outil statistique essentiel utilisé pour comprendre les relations entre plusieurs variables dans un ensemble de données.
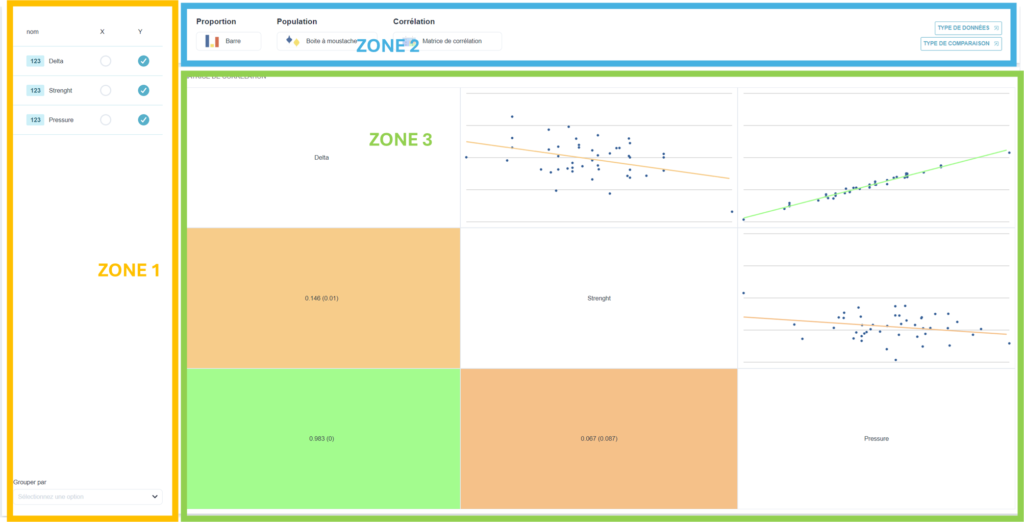
- Mettre dans la grille des données quantitatives de plusieurs colonnes Y. Dans l’exemple on souhaite trouver la corrélation entre les réponses Y1=”Delta”, Y2=“la force” et Y3=“Pression”
- Cliquer sur le menu “Statistiques inférentielles”.
- Dans la zone 1, choisir en Y les colonnes Y1=”Delta”, Y2=“la force” et Y3=“Pression”.
- Dans la zone 2, choisir le type de vos données. Par défaut, si les plusieurs colonnes choisies contiennent des valeurs quantitative, Ellistat va tracer les courbes de corrélation entre toutes les réponses deux à deux. En plus du sous-menu Corrélation, on à aussi la possibilité de choisir les sous-menus “Proportion” ou “Population” . 📝: choisir “Matrice de corrélation”
- Dans la zone 3, on obtient la matrice de corrélation qui contient dans la moitié au dessus de la diagonale tous les graphiques de corrélation de deux réponses deux à deux. Dans la diagonale de cette matrice on retrouve le nom des réponses. Et dans la moitié basse on trouve les coefficients de détermination R² et le seuil de significativité (P-value) .
Le schéma ci-dessous montre le graphique de corrélation, le R² et la P-value dans le cas des deux réponses Delta et Pression.
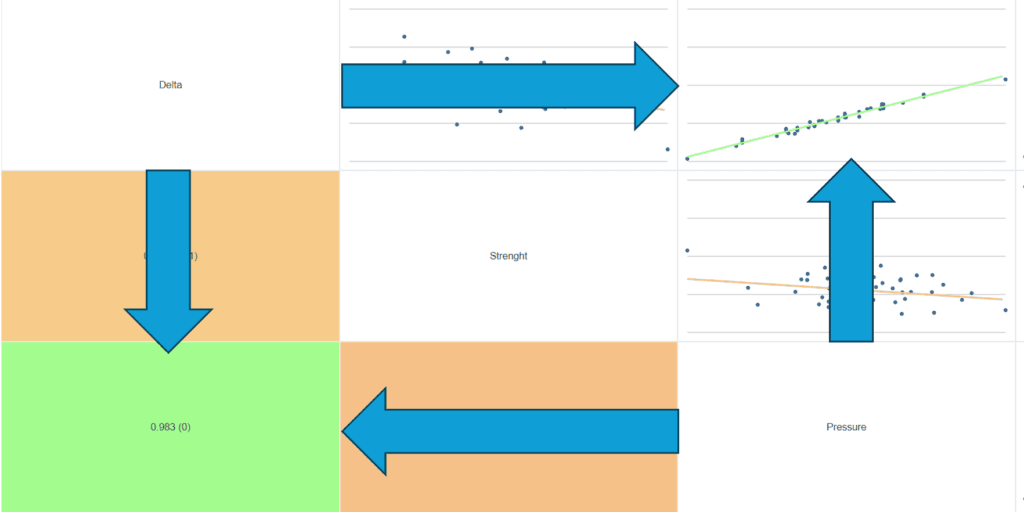
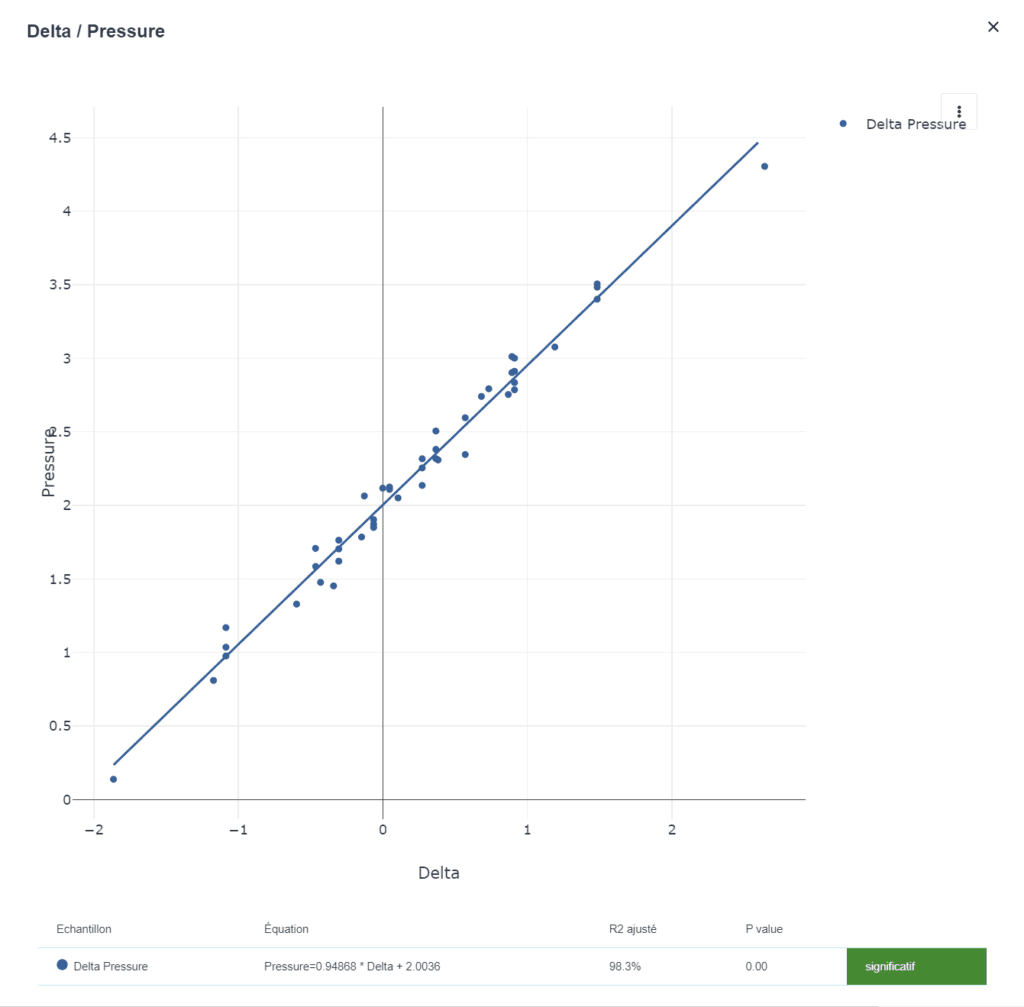
💡 Quand on clique sur un graphique, on retrouve un rapport d’une Analyse XY des deux réponses corrélées:
💡 Dans la moitié basse de la matrice de corrélation on retrouve deux valeurs :
R² (P-value).
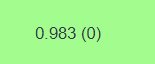
Exemple 2 : Trouver la corrélation entre plusieurs variables Y, avec l’ACP.
L’Analyse en Composantes Principales (ACP) est une méthode statistique utilisée pour réduire la dimensionnalité d’un jeu de données tout en conservant le maximum d’information possible. Cette technique est particulièrement utile lorsque l’on travaille avec des données multivariées (c’est-à-dire des données comportant plusieurs variables).
- Mettre dans la grille un jeu de données quantitatives de plusieurs colonnes Y. Dans l’exemple on souhaite réaliser une analyse ACP sur les données : Y1=”Delta”, Y2=“la force”, Y3=“Pression”, Y4=”Pression 2”, Y5=”Pression 3”
- Cliquer sur le menu “Statistiques inférentielles”.
- Dans la zone 1, choisir en Y les colonnes Y1=”Delta”, Y2=“la force” et Y3=“Pression”, Y4=”Pression 2”, Y5=”Pression 3”.
- Dans la zone 2, choisir le type de vos données. Appuyer sur le sous-menu “corrélation” et choisir “ACP”. En plus de ce sous-menu, on a aussi la possibilité de choisir les sous-menus “Proportion” ou “Population” . 📝: choisir “ACP”
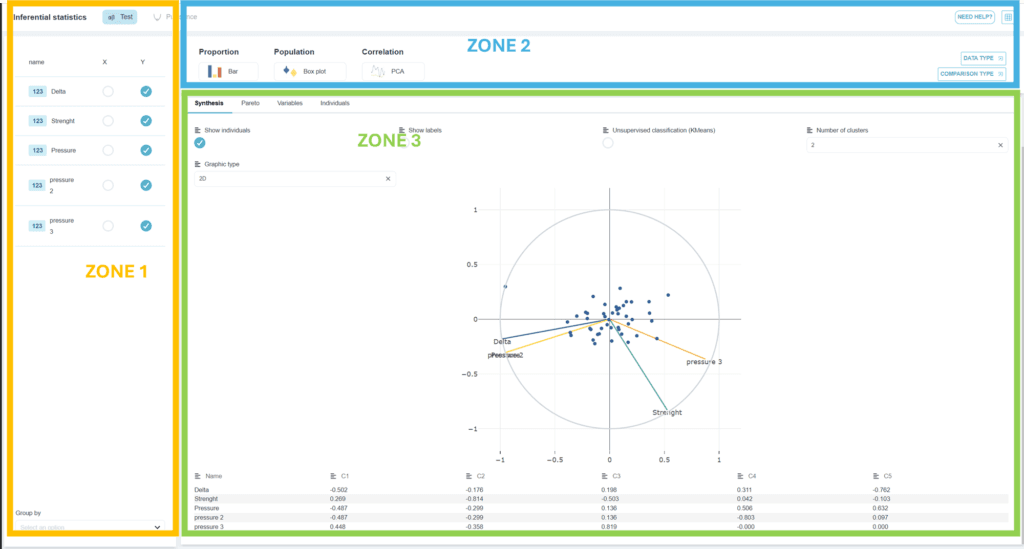
- Dans la zone 3, on obtient la projection des différentes réponse dans le plan composé des vecteurs principaux C1 (en abscisse) et C2 (en ordonnées).
💡 Dans la partie haute de la zone 3, il y a deux outils utilisés pour choisir un des facteurs du tableur:
Avec l’outil “Label” :
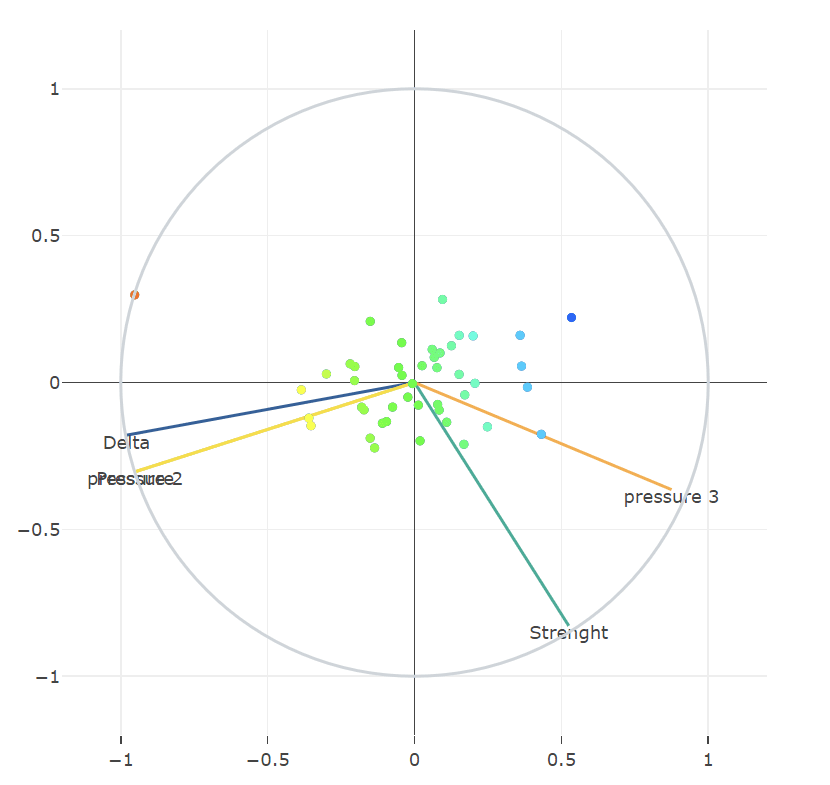
Il y a la possibilité de voir la variation des individus en fonction du facteur choisi . Cela permettrait d’appliquer un code couleur sur les individus en fonction de la variable choisie. Le cas suivant présente les résultats obtenus dans le cas du label = “Delta”. On constate que plus les individus qui ont un delta fort sont en orange/ jaune. Et que les individus qui ont un delta faible sont en bleu.

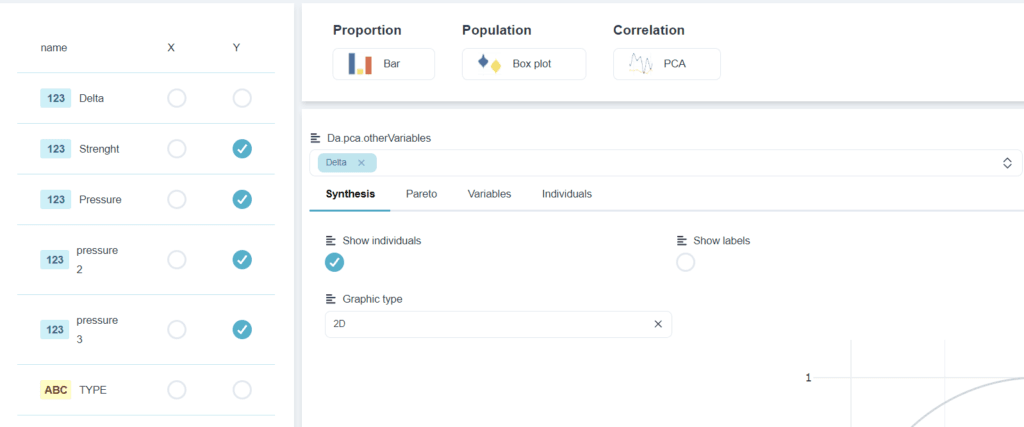
L’outil “autre variable”
Il est utilisé pour tracer un facteur sans le prendre en compte pour la détermination des vecteurs principaux. Attention ! Pour que cette fonctionnalité fonctionne il ne faut pas cocher le facteur dans les zones 1 et 3 en même temps. Il faut le cocher uniquement dans la zone 3. Ici, l’exemple du facteur “Delta” (voir la figure ci-dessous). Cette variable peut être soit une variable quantitatives ou soit une variable qualitative
Que ça soit l’option ”Label” ou l’option “autre variable” les variables choisies peuvent être des variables quantitatives ou des variables qualitatives.
💡 Dans la partie du milieu de la zone 3, on peut choisir plusieurs onglets:

L’onglet “Synthèse”:
Dans cet onglet on retrouve le graphique, les menus d’affichage des individus dans le graphique, le paramétrage de la classification et le tableau des vecteurs principaux.
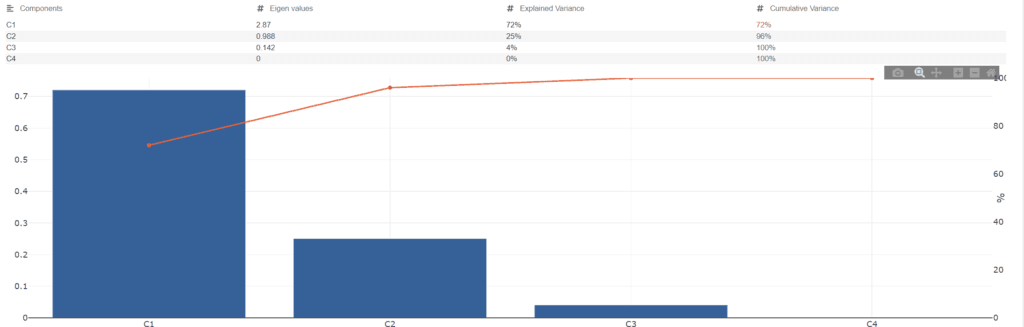
L’onglet Pareto :
Dans cet onglet on retrouve le diagramme Pareto qui exprime la contribution de chaque vecteur principal.
L’onglet “variable” :
Dans cet onglet on retrouve le degrés de significativité de corrélation entre les variables et les différents axes principaux (C1, C2,…). une P-value<0.05 signifie que la corrélation entre la variable et le vecteur principal est significative. (voir le tableau ci-dessous)

L’onglet “valeur individuelles” :
Dans cet onglet on retrouve le coordonnées des individus dans l’espace des vecteurs principaux.
Exemple 3 : La carte T² de Hotelling
La carte T² de Hotelling est un outil statistique utilisé pour le contrôle de la qualité multivariée et l’analyse de données. Ils permettent de surveiller des processus avec plusieurs variables simultanément. Elle est une extension multivariée des cartes de contrôle Shewhart, qui se concentrent sur une seule variable. Le T² de Hotelling est souvent utilisé dans des contextes où plusieurs caractéristiques de qualité doivent être surveillées en même temps. Par exemple dans le domaine de la fabrication, de la biologie, et de l’ingénierie.
- Mettre dans la grille des données quantitatives de plusieurs colonnes Y. Dans l’exemple on souhaite surveiller les données suivantes simultanément : Y1=”Delta”, Y2=“la force”, Y3=“Pression”, Y4=”Pression 2”, Y5=”Pression 3”
- Cliquer sur le menu “Statistiques inférentielles”.
- Dans la zone 1, choisir en Y les colonnes Y1=”Delta”, Y2=“la force” et Y3=“Pression”, Y4=”Pression 2”, Y5=”Pression 3”.
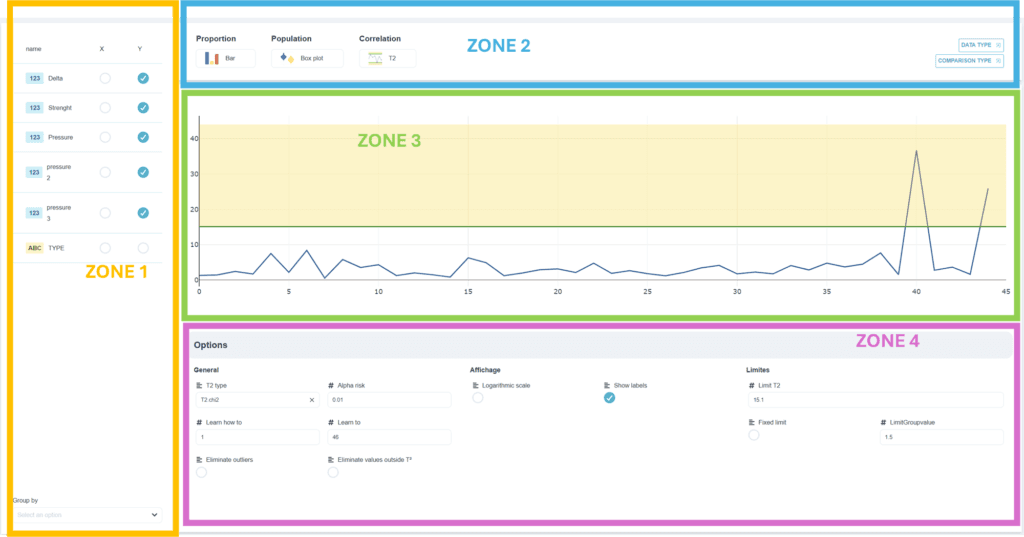
- Dans la zone 2, choisir le type de vos données. Appuyer sur le sous-menu “corrélation” et choisir “T²”. En plus de ce sous-menu, on a aussi la possibilité de choisir les sous-menus “Proportion” ou “Population” . 📝: choisir “T²”
- Dans la zone 3, on obtient la carte de contrôle T² avec les valeurs individuelles et les limites de contrôle.
- Dans la zone 4, on retrouve les différentes options comme les paramètres généraux de la carte, les options d’affichage et le calcul des limites de contrôle.
💡 Dans la partie du milieu de la zone 4, on peut paramétrer plusieurs options:
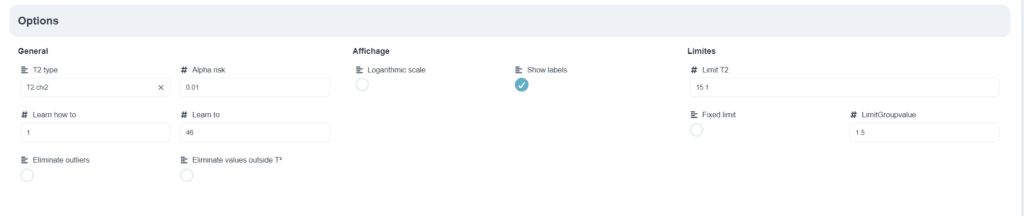
- “Général”: Avec cette option on peut choisir le type calcul de la carte de contrôle (classique, Sullivan, et Chi-2). On peut aussi choisir le niveau du risque alpha et déterminer les données pour l’apprentissage.
- “Affichage” : Avec cette option on peut transformer l’ordonnée en échelle logarithmique et appliquer un Label sur les données.
- “Limites” : Avec cette option on peut changer la limite de contrôle en la fixant manuellement.
