Ebben a cikkben a különböző képességindexek, különösen a Cp, Pp és Ppk kiszámítását nézzük meg.
Ahhoz, hogy teljes mértékben értékelni tudjuk egy folyamat képességét, az idő fogalma különösen fontos, mivel kétféle változékonyság létezik:
- Rövid távú változékonyság: amikor két alkatrészt egymás után gyártanak, ez a két alkatrész nem lesz teljesen egyenértékű a gép belső ingadozásai miatt. Ez a rövid távú változékonyság elsősorban a géptől függ.
- Hosszú távú változékonyság: ha ugyanazt a folyamatot hosszabb időn keresztül gyártják, maga a gép is kiesik a beállításból, és a sorozatváltozások, az anyagtételek változása stb. új variációs forrásokat eredményez. Ez a hosszú távú változékonyság a géptől, de számos külső változékonysági forrástól és a folyamat irányításának módjától is függ.
Példa
Ennek illusztrálására nézzük meg a következő termelési diagramot:
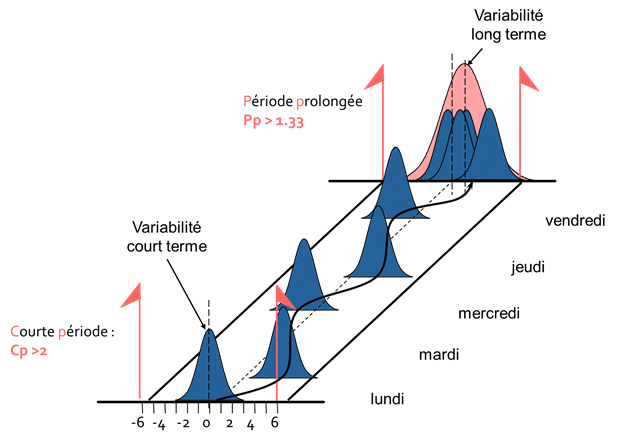
A heti termelés a hét különböző napjainak termeléséből adódik. Amint azonban a fenti ábra is mutatja, a hét különböző napjain a termelési feltételek nem egyenértékűek. A folyamat központosítása nem azonos a hétfői, keddi stb. termelés között...
Ennek eredményeként láthatjuk, hogy az egész hétre vonatkozó változékonyság (piros görbe) nagyobb, mint a rövid idő alatt megfigyelt változékonyság, mivel kevesebb olyan jelenséget vesz figyelembe, amely változékonyságot okozhat, mint például a kiigazítás vagy az anyagcsere.
A folyamat képességét tehát kétféleképpen lehet jellemezni, a megfigyelt változékonyság típusától függően: rövid távú cp és hosszú távú pp.
Rövid távú képességi index Cp
Rövid távú CpRövid távú képesség: A rövid távú képesség a folyamat azon képességének jellemzésére szolgál, hogy jó alkatrészeket tudjon előállítani, figyelembe véve csak a folyamat belső változékonyságát (a két egymást követő alkatrész közötti változékonyságot). A rövid távú képességet Cp-vel jelöljük, és a következőképpen számítjuk ki: :
Cp= \frac{\text{toleranciaintervallum}}{6*\text{rövid távú szórás}}= \frac{\text{toleranciaintervallum}}{6*\sigma_{\text{rövid távú}}}
Általában azt szeretnénk, hogy :
Cp > 2
Hosszú távú képességindex Pp
Hosszú távú PpHosszú távú képesség: A hosszú távú képességet annak jellemzésére használják, hogy a folyamat képes-e hosszú időn keresztül jó alkatrészeket gyártani, azaz figyelembe véve az esetlegesen bekövetkező kiigazításokat és folyamatmódosításokat. A hosszú távú képességet Pp-vel jelöljük, és a következőképpen számítjuk ki: :
Pp=\frac{toleranciaintervallum}{6∗hosszú távú szórás}=\frac{toleranciaintervallum}{6∗σ_{hosszú távú}}
Általában azt szeretnénk, hogy :
Pp > 1.33
Mivel a hosszú távú képesség több változékonysági forrást vesz figyelembe, mint a rövid távú képesség, szükségszerűen :
\text{hosszú távú szórás} < \text{rövid távú szórás}
És így
Pp < Cp
Ha ez nem így van, az nem azt jelenti, hogy a rövid távú szórás nagyobb, mint a hosszú távú, hanem azt, hogy a szórás nem stabil az idő múlásával.
A Cp, Pp, Ppk képességmutatók kiszámításának módszerei
Amint az imént láttuk, a Cp és a Pp kiszámítása ugyanazon képlet alapján történik. A Cp és a Pp azáltal különbözik, hogy a változékonyságot milyen időszakokra vonatkozóan számítják ki. A Cp és Pp kiszámítására többféle módszer létezik.
módszer: Több minta rendszeres időközönkénti vételével
Az első módszer a rövid és hosszú távú változékonyság kiszámítására az, hogy rendszeres időközönként több mintát veszünk.
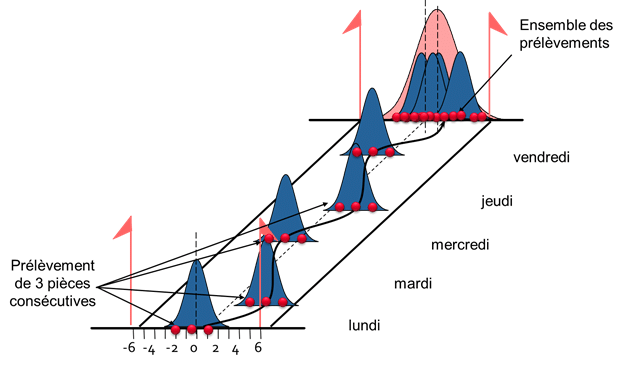
Rövid távú változékonyság : A rövid távú változékonyságot az összes minta sorozaton belüli szórása alapján számítják ki:
\sigma_{\text{rövid távon}}=\sigma_{\text{intra sample}}
Hosszú távú változékonyság : A folyamat egy jellemző időszakában 50 alkatrészből vesznek mintát, hogy figyelembe vegyék a folyamatváltozások többféle forrását, mint például a beállítások, szerszámcserék, anyagváltozások stb:
\sigma_{\text{long term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}
Példa: A következő mintát vesszük
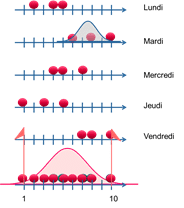
A tűrésintervallum [1 ;10].
A sorozaton belüli szórás kiszámítása :
\sigma_{\text{short term}}=\sigma_{\text{intra sample}}=1.7321
Az összes alkatrész szórását kiszámítjuk:
\sigma_{\text{long term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}=2.6904
Ebből következtethetünk :
Cp= \frac{\text{tolerancia intervallum}}{6*\text{rövid távú szórás}}= \frac{\text{tolerancia intervallum}}{6*\sigma_{\text{rövid távú}}= \frac{9}{6*1.7321}=0.87
Pp= \frac{\text{tolerancia intervallum}}{6*\text{hosszú távú szórás}}= \frac{\text{tolerancia intervallum}}{6*\sigma_{\text{hosszú távú}}= \frac{9}{6*2.6904}=0.56
Ppk=\frac{Min(\text{tolerancia max}-\mu,mu-\text{tolerancia min})}{3*\text{hosszú távú szórás}}= \frac{4.33}{3*2.6904}=0.54
módszer: Két külön minta vételével
A rövid és hosszú távú változékonyság kiszámításának második módszere két külön minta vétele.
- Rövid távú változékonyság: a folyamat rövid távú változékonyságának kiszámításához 50 egymást követő darabot veszünk kiigazítás nélkül. A rövid távú változékonyság kiszámítása a következő módon történik: :
\sigma_{\text{short term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}
- Hosszú távú változékonyság: 50 alkatrészből vesznek mintát a folyamat egy jellemző időszakában, hogy figyelembe vegyék a folyamat többféle variációs forrását, mint például a beállítások, szerszámváltások, anyagváltozások stb:
\sigma_{\text{long term}}=\sigma_{\text{all sample}}=\sqrt{\sum_{}^{}(\frac{^{(x_{i}-\mu)^{2}}}{n-1})}

