Az R&R garanciát a mérési folyamat minősítésére használják. Ez annak ellenőrzését jelenti, hogy a mérési folyamat változékonysága összeegyeztethető-e a mérendő mennyiség változékonyságával.
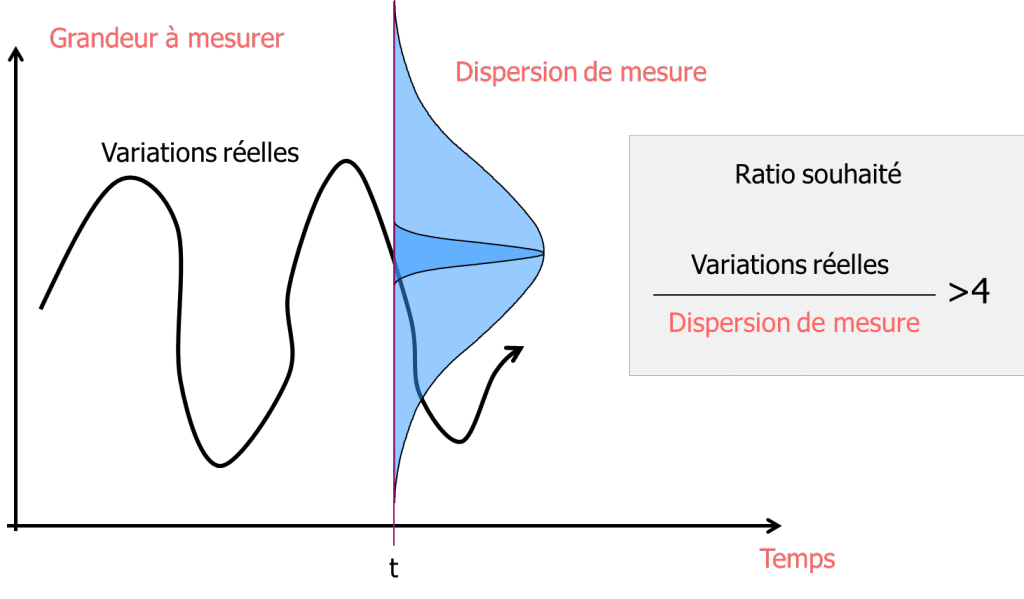
Szükségesnek tartják, hogy az alkatrészek változékonysága és a mérés változékonysága között 4-es arány legyen. Ezt az arányt Cpc termelésként fejezik ki:
\text{Cpc termelés}=\frac{text{termelés szórás}}{text{mérés szórás}}
A gyártási Cpc ezért az alkatrészek eloszlásától függ. Ha azonban egy mérőműszert szeretnénk jellemezni, akkor azt szeretnénk, ha ez a jellemzés független lenne a gyártási szórástól. Ezért egy új típusú változót vezetünk be, amely lehetővé teszi, hogy a mérőműszert ne az alkatrészek szórása, hanem az alkatrészek tűrésintervalluma alapján jellemezzük.
Ugyanúgy, ahogy a képességek kiszámítása, a mérőműszer jellemzése is megtörténik:
- Vagy Cpc (Control Process Capability):
\text{Cpc}=\frac{\text{tolerancia intervallum}}{\text{mérési szórás}}> 4
- GRR% (Megismételhetőség és reprodukálhatóság):
{\text{GRR}=\frac{\text{mérési szórás}}{\text{tolerancia intervallum}}<\text{0.3}}
Mint látható, a két mutató ugyanazt a dolgot képviseli, és megvan a kapcsolat :
\text{GRR}=\frac{\text{1}}{\text{Cpc}}
Íme az általánosan elfogadott szabályok:
| Cpc | GRR% | |
|---|---|---|
| Elfogadhatatlan | <3 | >30% |
| Folyamathatár | >3 és < 4 | 20% |
| Elfogadható | >4 | <20% |
| Kiváló | >8 | <10% |
Egy mérőműszer szórásának kiszámítása
A mérési folyamat szórásának kiszámításához ismételhetőségi és reprodukálhatósági vizsgálatot alkalmaznak.
Az ismételhetőségi és reprodukálhatósági vizsgálat célja a mérési folyamat általános szórásának jellemzése azáltal, hogy elválasztja az ismételhetőséget (azaz a mérési ismétlés szórását) a reprodukálhatóságtól (azaz a több kezelő közötti különbséget).
A teszt elvégzéséhez szükség van :
Szabványos vizsgálat: 3 kezelő egyenként 10 rész 3 alkalommal történő mérése.
Gyorsteszt: 3 operátor egyenként 10 részből egyenként 1 alkalommal mér (ez a teszt nem különíti el a megismételhetőséget és a reprodukálhatóságot).
A mérések elvégzése után a mérőközeg szórásának kiszámítására két módszer áll rendelkezésre:
ANAVAR módszer : Pontosabb módszer, amely kiszámítja az ismételhetőséget és a reprodukálhatóságot, és kimutatja, hogy vannak-e kölcsönhatások az alkatrészek és a kezelők között.
RANGE módszer : Egy közelítő módszer, amely könnyen kiszámítható egy Excel-táblázattal, de amely nem érzékel semmilyen alkatrész/üzemeltető kölcsönhatást.
Javasoljuk, hogy tartsa meg az ANAVAR számítási módszert, mivel ez a legpontosabb.
Tartomány módszer
A tartománymódszert különösen az iparban használják, mivel számításai könnyen elvégezhetők kézzel.
Ezzel a módszerrel kiszámítható a mérési folyamat ismételhetősége és reprodukálhatósága. Nem teszi azonban lehetővé a kölcsönhatás kiszámítását, ami korlátozza alkalmazási körét. Az ebben a módszerben végzett számítások a mintán belüli standard eltérés kiszámításán alapulnak a tartományoktól.
A számítási elv a következő:
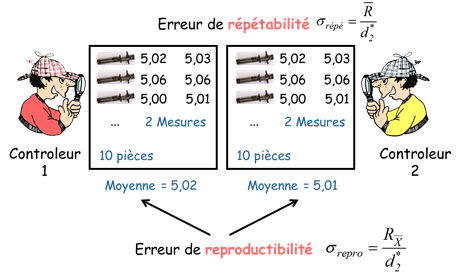
Az egyes kezelők által az egyes alkatrészeken végzett összes mérés egy mintának minősül. Ily módon a mintán belüli változékonyság a mérési folyamat megismételhetőségét jelenti, amelyet a következők szerint számítunk ki: :
\sigma_{repetablity}=\frac{\overline{R}}{d_{2}^{*}}
Ezután az egyes operátorok méréseinek átlagát tekintjük mintának. Ez lehetővé teszi a mérési folyamat reprodukálhatóságának kiszámítását :
\sigma_{operator}=\frac{R_{\overline{X}}}{d_{2}^{*}}
ANAVAR módszer
La ANAVAR módszer összetettebb:
A GRR és a Cpc kiszámításához az ANAVAR módszerrel a Fisher-tesztet használjuk:
| A változékonyság forrásai | Négyzetek összege | Szabadságfok | Átlagos négyzet | F-statisztikák |
|---|---|---|---|---|
| Üzemeltető | SSA | a-1 | \text{MSA}=\frac{\text{SSA}}{\text{a-1}} | \text{F}=\frac{\text{MSA}}{\text{MSE}} |
| Alkatrészek | SSB | b-1 | \text{MSB}=\frac{\text{SSB}}{\text{b-1}} | \text{F}=\frac{\text{MSB}}{\text{MSE}} |
| Interakció (üzemeltető/rész) | SSAB | (a-1)(b-1) | \text{MSAB}=\frac{\text{SSAB}}{\text{(a-1)(b-1)}} | \text{F}=\frac{\text{MSAB}}{\text{MSE}} |
| Műszer | SSE | ab(n-1) | \text{MSE}=\frac{\text{SSE}}{\text{ab(n-1)}} | |
| Összesen | TSS | N-1 |
a:
- a = az üzemeltetők száma
- b = darabszám
- n = az ismétlések száma
- N = a mérések teljes száma = abn
\text{SSA}=\sum^{a}{\frac{Y_{i}^{2}}{\text{bn}}}-\frac{Y_{**}^{2}}{N}
\text{SSB}=\sum^{b}{\frac{Y_{i}^{2}}{\text{an}}}-\frac{Y_{**}^{2}}{N}
\text{SSAB}=\sum^{a}\sum^{b}{\frac{Y_{ij}^{2}}{n}}-\frac{Y_{**}^{2}}{N}-\text{SSA}-\text{SSB}
\text{TSS}=\sum^{a}\sum^{b}\sum^{n}Y_{ijk}^{2}-\frac{Y_{**}^{2}}{N}
\text{SSE}=\text{TSS}-\text{SSA}-\text{SSB}-\text{SSAB}
A mérési folyamat ismételhetőségét a következő adja meg: :
\text{Répétabilité}=5.15\sqrt{\text{MSE}}
A mérési folyamat reprodukálhatóságát a következő adja meg: :
\text{Reproductibilité}=5.15\sqrt{\frac{\text{MSA}-\text{MSAB}}{\text{bn}}}
A kölcsönhatás a következővel adott:
\text{Intéraction}=5.15\sqrt{\frac{\text{MSAB}-\text{MSE}}{\text{n}}}
A mérési folyamat változékonyságát a következő adja meg
\text{Diszperzió}=5.15\sqrt{text{Megismételhetőség}^2+text{Megismételhetőség}^2+text{Interpretáció}^2}
Végül kiszámítjuk :
\text{GRR}=frac{Dispersion}{IT}
Ezt a módszert ezért sokkal bonyolultabb megvalósítani, de lehetővé teszi, hogy a kölcsönhatás mint a szórás forrása kiszámítható legyen, ami a RANGE módszerrel nem lehetséges. Ezért pontosabb.