A normalitás vizsgálatához többféle teszt is használható annak a hipotézisnek az igazolására vagy érvénytelenítésére, hogy az érmék eloszlása normális eloszlást követ. A leggyakrabban használt tesztek a következők:
- A Chi2 teszt
- Az Anderson-Darling teszt
Normalitásvizsgálat a Chi2-teszt segítségével
Az eloszlás normalitásának ellenőrzéséhez az első megérzésünk az lenne, hogy a megfigyelt változók eloszlásának hisztogramját ábrázoljuk. Ezután összehasonlítanánk, hogy ez a hisztogram jobban vagy kevésbé hasonlít-e a Gauss-görbe szokásos.
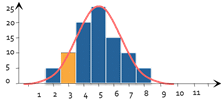
Pontosan ez az elv áll a Chi2 teszt mögött. Ez az intuíciót kiegészíti egy kis adag statisztikai számítással. Az elv a következő:
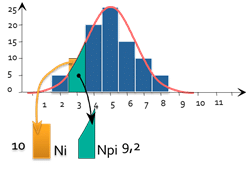
d_i=\frac{(N_i-NP_i)^{2}}{NP_i}
A hisztogram minden egyes sávjára kiszámíthatjuk :
- Ni : A ténylegesen megfigyelt alkatrészek száma (ebben az esetben 10).
- Npi: Az elméletileg megfigyelt részek száma, ha az eloszlás normális lenne (itt 9,2).
- di a "rosszul elhelyezett alkatrészek számát" jelöli.
Ezután kiszámítjuk
D=\sum_{}^{}D_i
és kiderül, hogy D egy n-2 szabadsági fokú eloszlási törvényt követ (N az osztályok száma). Ezután kiszámíthatjuk, hogy milyen valószínűséggel kapunk ilyen értéket.
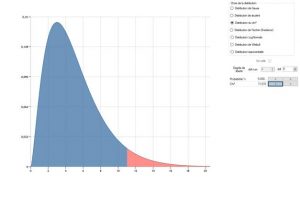
Például egy 7 osztályt tartalmazó hisztogram esetében, ha kiszámítottuk a 11,07-es D értéket, akkor kiszámítjuk, hogy 5% van ahhoz, hogy ilyen vagy ennél több értéket kapjunk, ha a részek eloszlása valóban normális.
A vizsgálat eredménye tehát 5% lesz, és az általános következtetés a következő:
- Ha X < 5%: a változók eloszlása nem tekinthető normális eloszlásúnak.
- Ha X >= 5%: a normalitás feltételezése elfogadható, és az eloszlás normális eloszlásúnak tekinthető.
Mi a teendő nem normális esetben?
A központi határértéktétel szerint :
Bármely rendszer, amely sok, egymástól független és azonos nagyságrendű tényező összegéből adódik, olyan eloszlási törvényt hoz létre, amely a normális eloszlás felé tendál.
De ellenkezőleg is gondolkodhatunk. Ha olyan eloszlást figyelünk meg, amely nem normális, akkor a tétel egyik hipotézise nem érvényes:
- 1. eset: a rendszer nem sok tényező összege: lehet sok tényező vagy más tényező szorzata. Ebben az esetben az eloszlási törvény eltérő lehet, és általában egy transzformáció (például az eredmény logaritmusának felvétele) visszaállítja a normális eloszlást.
- 2. eset: A tényezők nem függetlenek egymástól
- 3. eset: A tényezők nem azonos nagyságrendűek :
- Egy tényező felülmúlja a többit. Ebben az esetben meg kell találnunk a szóban forgó tényezőt, mert egyedül ez generálja a változékonyság egyik fő forrását.
- Egy kiugró szennyezi az eloszlást. Ebben az esetben meg kell találnunk a kiugró érték okát, és ki kell küszöbölnünk, ha az ok megmagyarázható.
Ebben a két esetben nem szükséges a megfigyelt változékonyságnak megfelelő eloszlási törvényt találni. Valójában ez az eloszlási törvény nem lesz idővel megismételhető, mivel egyetlen paraméterre vezethető vissza, így nem rendelkezik előrejelző tulajdonságokkal.
Ha a nemnormalitás eredete az 1. esetre vezethető vissza, akkor meg kell találnia a megfelelő eloszlási törvényt, különösen akkor, ha a tűréshatáron kívüli értékek százalékos arányát szeretné megjósolni. Ehhez használhatja a javasolt eloszlási törvényeket az ablak alján található az Adatelemzés modul hogy megnézzük, hogy az egyik eloszlás jól tükrözi-e a megfigyelt adatokat:

