A központi határértéktétel magyarázatához vegyük ezt a kiindulópontot. Isten nem kockázik" - mondta egyszer. A.Einstein a kvantummechanikáról, megkérdőjelezve a modern fizika egyik alapját. A 20. században végzett kísérletek azonban bebizonyították, hogy tévedett, és ma már elfogadott, hogy a világban minden megfigyelhető változót eloszlási valószínűségek szabályoznak, és Heisenberg bizonytalansági elvének hatálya alá tartoznak. A világ véletlenszerű...
A véletlen jelenségek megértése alapvető fontosságú a világ működésének megértéséhez. A statisztikai adatelemzés egyik központi tétele matematikailag is kimutatható: a központi határértéktétel.
Minden olyan rendszer, amely sok, egymástól független és azonos nagyságrendű tényező összegéből adódik, olyan eloszlási törvényt hoz létre, amely a normális eloszlás felé hajlik.
Ez a tétel megmutatja a normáleloszlás fontosságát egy megfigyelhető változó elemzése során. Ennek illusztrálására dobjunk egy kockát 1000-szer egymás után, és figyeljük meg az eredmények eloszlását:

Az eloszlás egyenletes eloszlást követ, azaz egyenlő esély van arra, hogy a kocka 1, 2, 3, 4, 5 vagy 6-ra esik. Az eloszlás nem hasonlít a normális eloszlásra.
Dobjunk 10 kockát 1000-szer egymás után, és nézzük meg, hogyan oszlik el ennek a 10 kockának az összege:
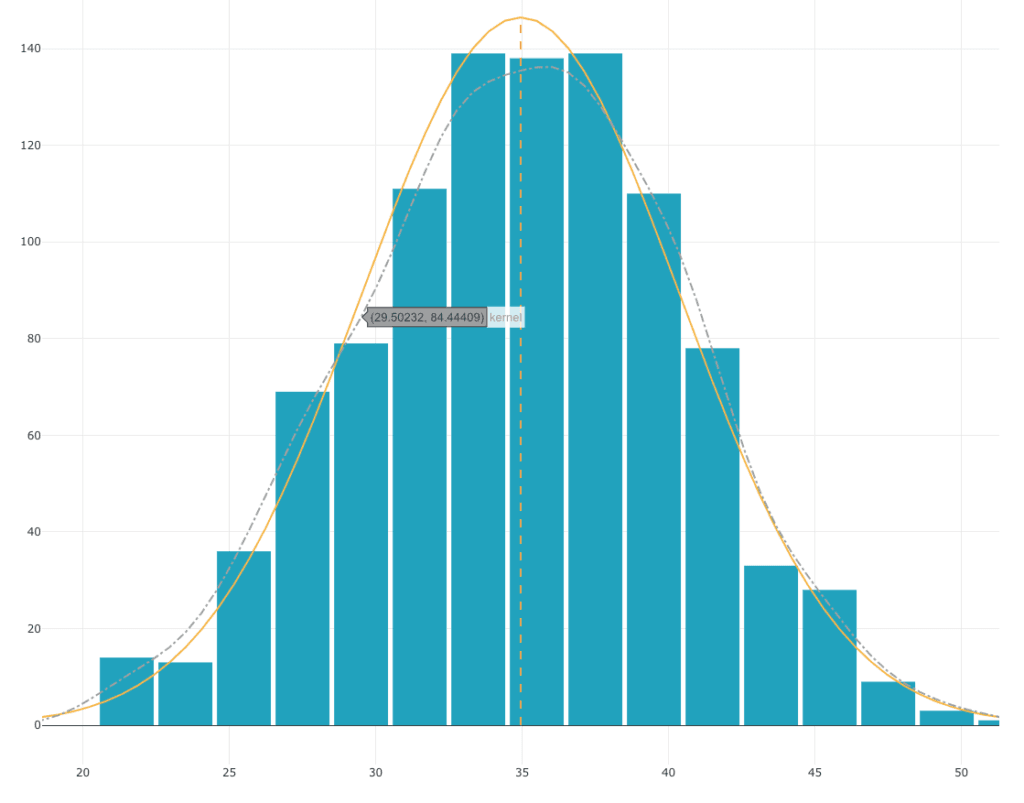
Bár minden kocka egyenletes eloszlást követ, a 10 kocka összegének eloszlása haranggörbét követ. Ez az eloszlás nagyon közel áll a normális eloszláshoz.
Valóban, ha a központi határértéktételt követjük :
- Van egy rendszerünk
- Sok tényező összegéből adódik (ebben az esetben 10 kocka összegéből).
- egymástól függetlenek (az egyik kocka eredménye nem befolyásolja a másik kocka eredményét).
- Az egyes kockák nagyságrendje egyenértékű
Az e rendszer által generált eloszlás a normális eloszlás felé hajlik. Mindent egybevetve, ez meglehetősen intuitív. Amikor 10 kockát dobunk, csak egyetlen olyan kombináció van, amely 10-es eredményt ad (az összes kocka 1-esre esik), míg több ezer olyan kombináció van, amely 35-ös eredményt ad. Ennek eredményeképpen a 35-öshöz közeli eredmények sokkal valószínűbbek, mint az olyan szélsőséges eredmények, mint a 10 vagy a 60. A kapott eloszlási törvény tehát közel áll a normális eloszlási törvényhez.
Az általunk általában megfigyelt rendszerek ilyen típusú eloszlással rendelkeznek, mivel megfelelnek a központi határértéktétel feltételezéseinek. Vegyük egy alkatrész megmunkálásának példáját:
- Ez egy olyan rendszer, amely egy jellemzőt hoz létre.
- A jellemzőnek a céltól való eltérése számos tényező (rezgések, az anyag keménysége, a szerszám pozicionálási hibája stb. ....) összegéből adódik.
- A tényezők függetlenek egymástól (a gép rezgései nem befolyásolják az anyag keménységét).
- Ezen eltérések nagyságrendje a következővel egyenértékű
Az alkatrészek eloszlása tehát a normális eloszlás felé tendál, amit akkor figyelhetünk meg, amikor alkatrészek sorozatát mérjük.
