Adatsorok elemzésekor néha találkozunk olyan értékekkel, amelyek nem tűnnek az adatok normális eloszlásának részének. Ezeket a pontokat kiugró értékeknek nevezzük, és mint általában, nem szabad mindig az intuíciójára hagyatkoznia, hogy felismerje, hogy egy érték kiugró érték-e. Vannak olyan tesztek, amelyek képesek kiemelni őket, és az olyan statisztikai szoftverek, mint például a(z) Ellistat hogy segítsen a számításokban.
Statisztikai szempontból a kiugró érték olyan érték, amely nem tartozik az adatok normális eloszlásához. Ez származhat :
- Mérési vagy másolási hiba (a tizedesvessző elfelejtése).
- Különleges ok, például ha egy darabot nem mostak meg a mérés előtt.
A normális eloszlás tulajdonságait használó valamennyi statisztikai számítás (statisztikai tesztek, képességszámítások, tűréshatáron kívüli % számítások) nagyon érzékeny a kiugró értékek jelenlétére, ezért fontos, hogy megértsük eredetüket és kiküszöböljük őket, mielőtt ezeket a számításokat használnánk. Használhatók nem parametrikus statisztikai tesztek is, amelyek sokkal kevésbé érzékenyek a kiugró értékekre.
Két fő tesztet használnak:
- Dixon tesztje : nagyon érdekes, ha az adatok száma alacsony (<30)
- Grubbs teszt minden esetben használható.
Dixon tesztje
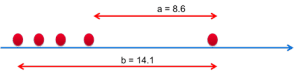
A Dixon-teszt alkalmazásához számítsa ki az arányt :
- b = A mérések teljes terjedelme (itt 14.1.)
- a = A kiugrónak vélt rész és a legközelebbi szomszédja közötti távolság (itt 8,6).
Az arányt %-ben kell kiszámítani.
Ezt a jelentést ezután összehasonlítjuk Dixon táblázatával:
| Darabszám | 3 | 5 | 10 | 16 | 20 | 30 |
| Maximális arány | 0.94 | 0.72 | 0.46 | 0.38 | 0.34 | 0.30 |
Ha az érték kisebb, mint a táblázat által javasolt maximális arány, akkor az érték nem számít kiugrónak. Itt a 62% arány 5 darab esetében kisebb, mint a 72%. A pont tehát nem számít kiugrónak.
Grubb-teszt
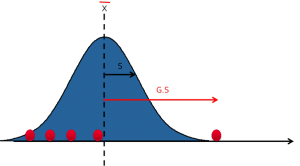
A Grubb-teszt használatához először kiszámítjuk :
- X: Az összes mérés átlaga
- S: Az összes mérés szórása
- G: a kiugrónak vélt érték és a G átlag közötti távolság.
G=\frac{(Value - X)}{S}
A kapott G értéket ezután összehasonlítjuk egy G határértékkel:
G_{limite}=\frac{N-1}{\sqrt{N}}.\sqrt{\frac{t^2_{\frac{a}{N},N-2}{}}{N-2 +t^2{}_{\frac{a}{n}}{,} N-2}}
Ha G>G határérték, az értéket kiugrónak tekintjük, és fordítva.


