Per spiegare il teorema del limite centrale, prendiamo questo come punto di partenza. Dio non gioca a dadi", ha detto una volta A.Einstein sulla meccanica quantistica, mettendo in discussione uno dei fondamenti della fisica moderna. Tuttavia, gli esperimenti condotti nel XX secolo hanno dimostrato che si sbagliava, e oggi si ammette che tutte le osservabili di questo mondo sono governate da probabilità di distribuzione e sono soggette al principio di indeterminazione di Heisenberg. Il mondo è casuale...
La comprensione dei fenomeni casuali è fondamentale per capire come funziona il mondo. Un teorema centrale dell'analisi statistica dei dati può essere dimostrato matematicamente: il teorema del limite centrale.
Qualsiasi sistema risultante dalla somma di molti fattori, indipendenti tra loro e di ordine di grandezza equivalente, genera una legge di distribuzione che tende a una distribuzione normale.
Questo teorema dimostra l'importanza della distribuzione normale nell'analisi della variabilità di un'osservabile. Per illustrarlo, lanciamo un dado per 1000 volte di seguito e osserviamo la distribuzione dei risultati:

La distribuzione segue una distribuzione uniforme, vale a dire che c'è la stessa probabilità che il dado cada su 1, 2, 3, 4, 5 o 6. La distribuzione non assomiglia a una distribuzione normale.
Lanciamo 10 dadi per 1000 volte di seguito e vediamo come si distribuisce la somma di questi 10 dadi:
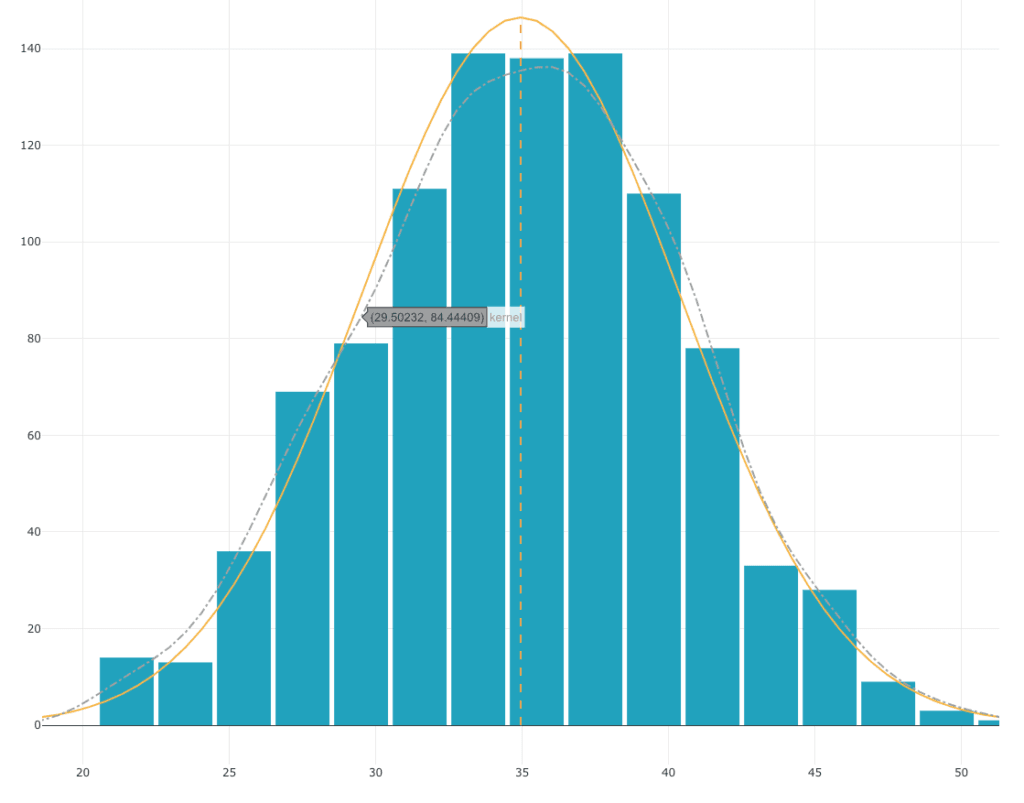
Sebbene ogni dado segua una distribuzione uniforme, la distribuzione della somma dei 10 dadi segue una curva a campana. Questa distribuzione è molto vicina a una distribuzione normale.
Infatti, se seguiamo il teorema del limite centrale :
- Abbiamo un sistema
- Risultato della somma di più fattori (in questo caso la somma di 10 dadi)
- Indipendenti l'uno dall'altro (il risultato di un dado non ha alcuna influenza sul risultato di un altro dado)
- L'ordine di grandezza di ciascuno dei dadi è equivalente
La distribuzione generata da questo sistema tende a una distribuzione normale. Tutto sommato, questo è abbastanza intuitivo. Quando si lanciano 10 dadi, esiste una sola combinazione che produce un risultato di 10 (tutti i dadi sono finiti sull'1), mentre esistono migliaia di combinazioni che producono un risultato di 35. Di conseguenza, i risultati vicini a 35 sono molto più probabili di quelli estremi, come 10 o 60. Di conseguenza, è molto più probabile che si verifichino risultati vicini a 35 rispetto a risultati estremi come 10 o 60. La legge di distribuzione ottenuta è quindi vicina alla legge di distribuzione di 35. La legge di distribuzione ottenuta si avvicina quindi a una legge di distribuzione normale.
I sistemi che osserviamo di solito hanno questo tipo di distribuzione, perché soddisfano le ipotesi del teorema del limite centrale. Prendiamo l'esempio della lavorazione di un pezzo:
- È un sistema che produce una caratteristica.
- La deviazione della caratteristica dall'obiettivo risulta dalla somma di molti fattori (vibrazioni, durezza del materiale, errore di posizionamento dell'utensile, ecc. ....).
- I fattori sono indipendenti l'uno dall'altro (le vibrazioni della macchina non hanno alcuna influenza sulla durezza del materiale).
- L'ordine di grandezza di queste deviazioni è equivalente a
La distribuzione dei pezzi tende quindi a una distribuzione normale, che è quella che si osserva quando si misura una serie di pezzi.
