Lorsque l’on analyse une série de données, il arrive que l’on se retrouve confronté à des valeurs qui nous semblent ne pas faire partie de la distribution normale des données. On appelle ces points des valeurs aberrantes et comme d’habitude, il ne faut pas toujours se fier à son intuition pour pouvoir détecter si une valeur est aberrante ou non, il existe des tests qui permettent de les mettre en évidence et des logiciels statistiques comme Ellistat pour vous aider dans les calculs.
D’un point de vue statistique, une valeur aberrante est une valeur qui n’appartient pas à la distribution normale des données. Elle peut provenir :
- D’une erreur de mesure ou de recopie (oubli de la virgule)
- D’une cause spéciale comme une pièce non lavée avant mesure.
L’ensemble des calculs statistiques utilisant les propriétés de la loi normale (tests statistiques, calcul de capabilité, calcul de % hors tolérance) est très sensible à la présence de valeurs aberrantes, il convient donc de comprendre leur origine et de les éliminer avant d’utiliser ces calculs. On pourra éventuellement utiliser les tests statistiques non paramétriques qui sont beaucoup moins sensibles aux valeurs aberrantes.
Deux tests sont principalement utilisés :
- Test de Dixon : très intéressant lorsque le nombre de données est faible (<30)
- Test de Grubbs : peut-être utilisé dans tous les cas.
Test de Dixon
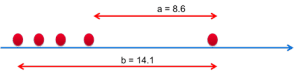
Pour utiliser le test de Dixon, on calcule le rapport :
- b = L’étendue globale des mesures (ici 14.1)
- a = La distance entre la pièce suspectée d’être une valeur aberrante et son plus proche voisin (ici 8.6)
Le rapport est calculé en %.
On compare ensuite ce rapport au tableau de Dixon :
| Nombre de pièce | 3 | 5 | 10 | 16 | 20 | 30 |
| Rapport maximum | 0.94 | 0.72 | 0.46 | 0.38 | 0.34 | 0.30 |
Si la valeur est inférieure au rapport maximum proposé par le tableau alors la valeur n’est pas aberrante. Ici le rapport de 62% pour 5 pièces est inférieur à 72%. Le point n’est donc pas une valeur aberrante.
Test de Grubb
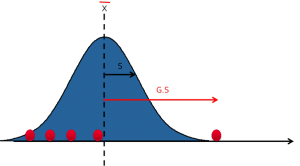
Pour utiliser le test de Grubb, on calcule dans un premier temps :
- X : La moyenne de l’ensemble des mesures
- S : L’écart-type de l’ensemble des mesures
- G : Distance entre la valeur suspectée d’être un point aberrant et la moyenne G.
G=\frac{(Valeur - X)}{S}
On compare ensuite la valeur de G obtenue à un G limite :
G_{limite}=\frac{N-1}{\sqrt{N}}.\sqrt{\frac{t^2_{\frac{a}{N},N-2}{}}{N-2 +t^2{}_{\frac{a}{n}}{,} N-2}}
Si G>G limite la valeur est considérée comme aberrante et inversement.


