Mithilfe des R&R-Pfands kann ein Messprozess qualifiziert werden. Das heißt, es wird überprüft, ob die Variabilität des Messprozesses mit der Variabilität der zu messenden Menge vereinbar ist.
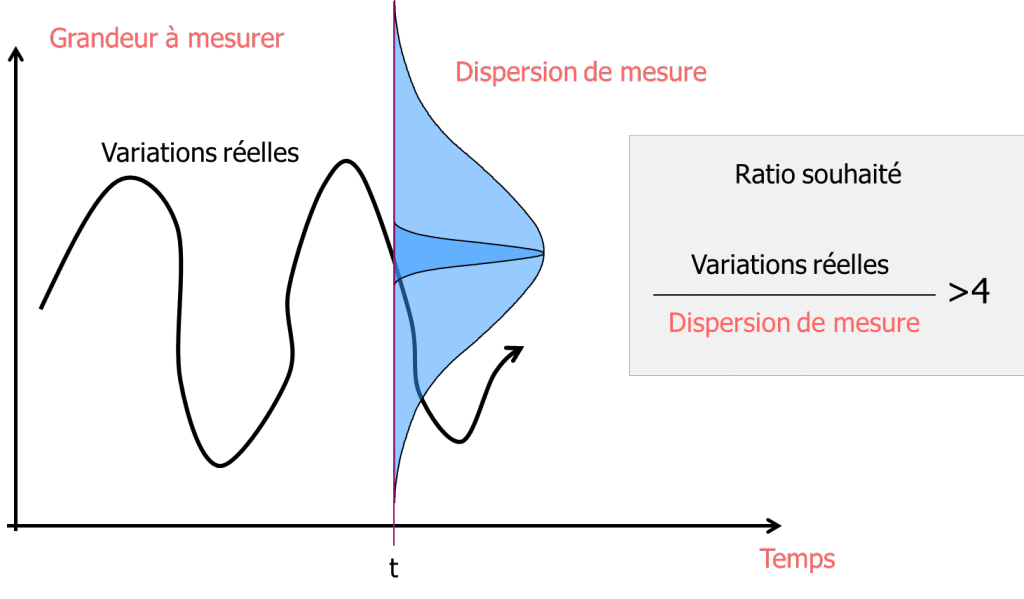
Es wird davon ausgegangen, dass ein Verhältnis von 4 zwischen der Variabilität der Teile und der Variabilität der Messung notwendig ist. Dieses Verhältnis wird als Cpc Produktion ausgedrückt:
\...::: www. SubCentral. de :::... ...::: präsentiert:::...
Der Cpc Produktion hängt also von der Streuung der Teile ab. Wenn man nun aber ein Messinstrument charakterisieren will, möchte man, dass diese Charakterisierung unabhängig von der Produktionsvariabilität ist. Wir werden daher einen neuen Variablentyp einführen, mit dem das Messinstrument nicht in Bezug auf die Teiledispersion, sondern in Bezug auf das Toleranzintervall der Teile charakterisiert werden kann.
Ähnlich wie bei der Berechnung einer Fähigkeit wird das Messinstrument charakterisiert :
- Entweder durch Cpc (Capability of the Control Process) :
\text{Cpc}=\frac{\text{tolerance interval}}{\text{measurement dispersion}}> 4
- Entweder durch den GRR% (Wiederholbarkeit und Reproduzierbarkeit) :
{][ Übersetzung ][ .....][ extreme ][.....][ extreme ][.....}
Wie Sie feststellen können, stellen die beiden Indikatoren dasselbe dar und man hat die Beziehung :
\text{GRR}=\frac{\text{1}}{\text{Cpc}}
Hier also die üblicherweise akzeptierten Regeln:
| Cpc | GRR% | |
|---|---|---|
| Inakzeptabel | <3 | >30% |
| Grenzprozess | >3 und < 4 | 20% |
| Akzeptabel | >4 | <20% |
| Ausgezeichnet | >8 | <10% |
Die Streuung eines Messinstruments berechnen
Um die Streuung eines Messverfahrens zu berechnen, wird ein Test auf Wiederholbarkeit und Reproduzierbarkeit verwendet.
Der Test auf Wiederholbarkeit und Reproduzierbarkeit zielt darauf ab, die gesamte Streuung des Messvorgangs zu charakterisieren, indem er trennt, was in den Bereich der Wiederholbarkeit fällt (d. h. die Streuung der Messwiederholung) und was in den Bereich der Reproduzierbarkeit fällt (d. h. ein Unterschied zwischen mehreren Bedienern).
Um diesen Test durchzuführen braucht man :
Standardtest: 3 Bediener messen jeweils 10 Münzen 3-mal.
Schnelltest: 3 Personen messen jeweils 10 Teile je 1 Mal (dieser Test trennt nicht zwischen Wiederholbarkeit und Reproduzierbarkeit)
Nachdem die Messungen durchgeführt wurden, gibt es zwei Methoden, um die Streuung des Messmittels zu berechnen:
ANAVAR-Methode : Eine genauere Methode, mit der sowohl die Wiederholbarkeit als auch die Reproduzierbarkeit berechnet und festgestellt werden kann, ob es Wechselwirkungen zwischen Teilen und Bedienern gibt.
RANGE-Methode : Näherungsweise Methode, die sich leicht mit einer Excel-Tabelle berechnen lässt, aber keine Möglichkeit bietet, eine mögliche Interaktion zwischen Teilen und Bediener zu erkennen.
Wir empfehlen Ihnen, die ANAVAR-Berechnungsmethode beizubehalten, da sie die genaueste ist
Methode Range
Die Range-Methode wird vor allem in der Industrie verwendet, da ihre Berechnungen leicht von Hand durchgeführt werden können.
Diese Methode ermöglicht es, die Wiederholbarkeit und Reproduzierbarkeit des Messprozesses zu berechnen. Sie ermöglicht jedoch keine Berechnung der Interaktion, was ihren Anwendungsbereich einschränkt. Die Berechnungen dieser Methode basieren auf der Berechnung einer Intra-Stichproben-Standardabweichung aus den Spannweiten.
Die Berechnung erfolgt nach folgendem Prinzip:
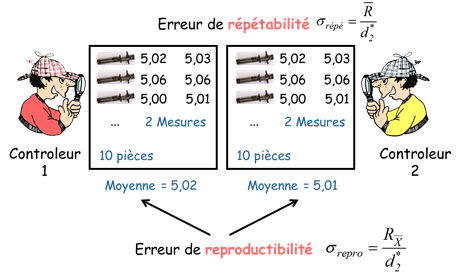
Man betrachtet die Gesamtheit der Messungen jedes Teils durch jeden Bediener als eine Stichprobe. Auf diese Weise stellt die Intra-Stichprobenvariabilität die Wiederholbarkeit des Messvorgangs dar, die man berechnet durch :
\sigma_{repetablity}=\frac{\overline{R}}{d_{2}^{*}}
Die Durchschnittswerte der Messungen jedes Bedieners werden dann als Stichprobe betrachtet. Dies ermöglicht es, die Reproduzierbarkeit des Messprozesses zu berechnen durch :
\sigma_{operator}=\frac{R_{\overline{X}}}{d_{2}^{*}}
ANAVAR-Methode
Die ANAVAR-Methode ist komplexer:
Um GRR und Cpc mit der ANAVAR-Methode zu berechnen, werden die statistischen Analysen des Fisher-Tests verwendet:
| Quellen der Variabilität | Summe der Quadrate | Grad der Freiheit | Mittelwert der Quadrate | F-Statistik |
|---|---|---|---|---|
| Operator | SSA | a-1 | \text{MSA}=\frac{\text{SSA}}{\text{a-1}} | \text{F}=\frac{\text{MSA}}{\text{MSE}} |
| Münzen | SSB | b-1 | \text{MSB}=\frac{\text{SSB}}{\text{b-1}} | \text{F}=\frac{\text{MSB}}{\text{MSE}} |
| Interaktion (Operator/Raum) | SSAB | (a-1)(b-1) | \text{MSAB}=\frac{\text{SSAB}}{\text{(a-1)(b-1)}} | \text{F}=\frac{\text{MSAB}}{\text{MSE}} |
| Instrument | SSE | ab(n-1) | \text{MSE}=\frac{\text{SSE}}{\text{ab(n-1)}} | |
| Gesamt | TSS | N-1 |
mit:
- a = Anzahl der Operatoren
- b = Anzahl der Stücke
- n = Anzahl der Wiederholungen
- N = Gesamtzahl der Messungen = abn
\text{SSA}=\sum^{a}{\frac{Y_{i}^{2}}{\text{bn}}}-\frac{Y_{**}^{2}}{N}
\text{SSB}=\sum^{b}{\frac{Y_{i}^{2}}{\text{an}}}-\frac{Y_{**}^{2}}{N}
\text{SSAB}=\sum^{a}\sum^{b}{\frac{Y_{ij}^{2}}{n}}-\frac{Y_{**}^{2}}{N}-\text{SSA}-\text{SSB}
\text{TSS}=\sum^{a}\sum^{b}\sum^{n}Y_{ijk}^{2}-\frac{Y_{**}^{2}}{N}
\text{SSE}=\text{TSS}-\text{SSA}-\text{SSB}-\text{SSAB}
Die Wiederholbarkeit des Messvorgangs ist gegeben durch :
\text{Répétabilité}=5.15\sqrt{\text{MSE}}
Die Reproduzierbarkeit des Messvorgangs ist gegeben durch :
\text{Reproductibilité}=5.15\sqrt{\frac{\text{MSA}-\text{MSAB}}{\text{bn}}}
Die Interaktion ist gegeben durch :
\text{Intéraction}=5.15\sqrt{\frac{\text{MSAB}-\text{MSE}}{\text{n}}}
Die Variabilität des Messprozesses ist gegeben durch
\text{Dispersion}=5.15\sqrt{\text{Répétabilité}^2+\text{Reproductibilité}^2+\text{Intéraction}^2}
Schließlich berechnen wir :
\c&H30D3F4&}} \c&H30D3F4&}}
Diese Methode ist also viel komplizierter zu implementieren, aber sie erlaubt es, die Interaktion als Quelle der Streuung zu berechnen, was die RANGE-Methode nicht kann. Sie ist daher genauer.