Népesség

Ellistat Adatelemzés a következő termékek teljes skáláját kínálja statisztikai tesztelés parametrikus és nem parametrikus tesztek mennyiségi adatok populációjának összehasonlítására. E statisztikai tesztek célja két vagy több populáció összehasonlítása, akár a pozíciók (például átlagok vagy mediánok), akár a szórások (varianciák) tekintetében.

A hipotézisvizsgálat két nagy kategóriába sorolható:

• Parametrikus tesztek (narancssárga színnel): Ezek a statisztikai tesztek feltételezéseket tesznek a populáció eloszlásának paramétereire, például az átlagra és a szórásra vonatkozóan, és olyan példákat tartalmaznak, mint a Student's t-teszt, az ANOVA és a lineáris regressziós teszt.
• Nem parametrikus tesztek (zölddel): Ezek olyan statisztikai tesztek, amelyek nem tesznek feltevéseket a populációs adatok eloszlásáról, és olyan példákat tartalmaznak, mint a Wilcoxon-, a Kruskal-Wallis- vagy a Friedman-teszt.

Az alábbi táblázat összefoglalja az Ellistat adatelemzésben elérhető összes statisztikai tesztet:

Az alábbi szakaszok részletezik az Ellistat adatelemzéssel elvégezhető statisztikai vizsgálatokat:

1. Statisztikai tesztek az átlagok összehasonlítására

Az átlagok összehasonlítása:

Az alábbi példák összefoglalják az átlagok összehasonlítására végzett összehasonlítások típusait.

Az alábbi linkek tartalmazzák az Ellistat Data Analysis által javasolt különböző átlag-összehasonlító elemzésekhez használt adatokat. Vegyük példának a következő adatokat

Független adatok 🇺🇸/ Données indépendantes🇫🇷 

Párosított adatok 🇺🇸/ Données appariées 🇫🇷 

Példa 1: Egy átlag és egy elméleti érték összehasonlítása :

Végezzen 1T tesztet, hogy összehasonlítsa az átlagot egy elméleti értékkel.

• Írja be a példa mennyiségi adatait a rácsba. A vizsgálat célja, hogy összehasonlítsuk az A szállító átlagos erejét 5 N-nal.
• Kattintson a "Következtetési statisztika" menüpontra.
• A 1. zónaválassza ki a mennyiségi adatokat tartalmazó oszlopot Y-ban.
• A oldalon. 2. zóna, válassza ki az adatok típusát. Alapértelmezés szerint, ha az oszlop minőségi értékeket tartalmaz, az Ellistat csak az "Arány" típust fogja javasolni, de ha az adatok mennyiségiak, az Ellistat a két típust, az "arányt" és a "népességet" fogja javasolni. 📝: válassza a "népesség" lehetőséget.
• A oldalon. 3. zónaa 2. zónában kiválasztott grafikához.
• A 4. zónaA szignifikancia eredménye (a jobb oldalon látható) az alábbi különböző statisztikákkal együtt. (Az átlag és az elméleti érték közötti különbség akkor szignifikáns, ha a P-érték kisebb, mint 0,05. Az alábbi esetben megállapíthatjuk, hogy a különbség szignifikáns). 📝: A tartalom 4. zónafügg az adatok típusától, amelyet a 2. zóna.

Példa 2: Két átlag összehasonlítása

Végezzen 2T tesztet két különböző átlag összehasonlítására.

• Írja be a példa mennyiségi adatait a rácsba. A vizsgálat célja az A és B beszállító átlagos erősségének összehasonlítása.
• Kattintson a "Következtetési statisztika" menüpontra.
• A 1. zónaHa az adatok 2 különböző oszlopban vannak, válassza ki az A és B oszlopot Y-ban. Ha az adatok egymásra vannak halmozva (egy szállító oszlop a szilárdság oszlop mellett), válassza a szilárdságot Y-nak és a szállítót X-nek.
• A oldalon. 2. zóna, válassza ki az adatok típusát. Alapértelmezés szerint, ha az oszlop minőségi értékeket tartalmaz, az Ellistat csak az "Arány" típust fogja javasolni, de ha az adatok mennyiségiak, az Ellistat a két típust, az "arányt" és a "népességet" fogja javasolni. 📝: válassza a "népesség" lehetőséget.
• A oldalon. 3. zónaa 2. zónában kiválasztott grafikához.

• A 4. zóna. . a szignifikancia eredménye (a jobb oldalon jelenik meg) a különböző statisztikákkal együtt. (A két A és B átlag közötti különbség akkor szignifikáns, ha a P-érték kisebb, mint 0,05. Az alábbi esetben megállapíthatjuk, hogy a különbség nem szignifikáns). 📝: A tartalom 4. zóna függ az adatok típusától, amelyet a 2. zóna.

Példa 3: Három vagy több átlag összehasonlítása

Végezzen ANOVA (varianciaanalízis) tesztet 3 vagy több átlag összehasonlítására.

• Írja be a példa mennyiségi adatait a rácsba. A vizsgálat célja az A, B és C szállítók átlagos erősségének összehasonlítása.
• Kattintson a "Következtetési statisztika" menüpontra.
• A 1. zónaVálassza ki az A, B és C oszlopokat Y-ban, ha az adatok 3 különböző oszlopban vannak. vagy ha az adatok egymásra vannak halmozva (egy szállítói oszlop az erősségeket tartalmazó oszlop mellett). válassza az erősséget Y-nak és a szállítót X-nek.
• A oldalon. 2. zóna, válassza ki az adatok típusát. Alapértelmezés szerint, ha az oszlop minőségi értékeket tartalmaz, az Ellistat csak az "Arány" típust fogja javasolni, de ha az adatok mennyiségiak, az Ellistat a két típust, az "arányt" és a "népességet" fogja javasolni. 📝: válassza a "népesség" lehetőséget.
• A oldalon. 3. zónaa 2. zónában kiválasztott grafikához.

• A 4. zóna. . a szignifikancia eredménye (a jobb oldalon jelenik meg) a különböző statisztikákkal együtt. (Az A, B és C átlagok közötti különbség akkor szignifikáns, ha a P-érték kisebb, mint 0,05. Az alábbi esetben megállapíthatjuk, hogy a különbség nem szignifikáns). 📝: A tartalom 4. zóna függ az adatok típusától, amelyet a 2. zóna.

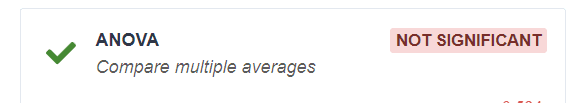
Példa 4: Párosított adatok

A statisztikával összefüggésben a párosított adatok (vagy párosított adatok) olyan adathalmazokra utalnak, amelyekben a megfigyeléseket párban gyűjtik. Minden megfigyelési pár általában meghatározott módon kapcsolódik egymáshoz, lehetővé téve az egyes párokon belüli két érték közvetlen összehasonlítását.

Példa:

• Hasonlítsa össze az átlagos keménységet a hőkezelés előtt és után.
• Hasonlítsa össze a fehérvérsejtszámot a kezelés előtt, az első adag kezelés után és a második adag kezelés után.

Párosított adatok átlagainak összehasonlítása.

Az Ellistat két megfelelő tesztet kínál a párosított adatok átlagainak összehasonlítására:

⇒ T-próba párosított adatok esetén két átlag esetében.

⇒ ANOVA párosított adatok esetén két vagy több átlag esetében.

Párosított adatok 🇺🇸/ Données appariées 🇫🇷 

2. Statisztikai tesztek a standard eltérések összehasonlítására

A standard eltérések összehasonlítása:

Az alábbi példák összefoglalják a standard eltérések összehasonlítására végzett összehasonlítások típusait.

Az alábbi linkek tartalmazzák az Ellistat Data Analysis által javasolt különböző szórás-összehasonlító elemzésekhez használt adatokat. Vegyük példaként a következő adatokat:

Független adatok 🇺🇸/ Données indépendantes🇫🇷 

Példa 1: Egy szórás és egy elméleti érték összehasonlítása :

Egy Chi-2 tesztegy szórás és egy elméleti érték összehasonlítása.

• Írja be a példa mennyiségi adatait a rácsba. A vizsgálat célja, hogy összehasonlítsuk az A szállító 1 N erősségének szórását.
• Kattintson a "Következtetési statisztika" menüpontra.
• A 1. zónaválassza ki a mennyiségi adatokat tartalmazó oszlopot Y-ban.
• A oldalon. 2. zóna, válassza ki az adatok típusát. Alapértelmezés szerint, ha az oszlop minőségi értékeket tartalmaz, az Ellistat csak az "Arány" típust fogja javasolni, de ha az adatok mennyiségiak, az Ellistat a két típust, az "arányt" és a "népességet" fogja javasolni. 📝: válassza a "népesség" lehetőséget.
• A oldalon. 3. zónaa 2. zónában kiválasztott grafikához.
• A 4. zónaA szignifikancia eredménye (a jobb oldalon látható) az alábbi különböző statisztikákkal együtt. (a szórás és az elméleti érték közötti különbség akkor szignifikáns, ha a P-érték kisebb, mint 0,05. Az alábbi esetben megállapíthatjuk, hogy a különbség szignifikáns). 📝: A tartalom 4. zónafügg az adatok típusától, amelyet a 2. zóna.

Példa 2: Két standard eltérés összehasonlítása.

Az Ellistat 2 tesztet kínál a standard eltérések összehasonlítására:

⇒Fischer-tesztkét különböző standard eltérés összehasonlítására.

⇒A Levene-tesztkét vagy több standard eltérés összehasonlítása.

• Írja be a példa mennyiségi adatait a rácsba. A vizsgálat célja, hogy összehasonlítsa az A és a B szállító erősségeinek szórásait.
• Kattintson a "Következtetési statisztika" menüpontra.
• A 1. zónaHa az adatok 2 különböző oszlopban vannak, válassza ki az A és B oszlopot Y-ban. Ha az adatok egymásra vannak halmozva (egy szállító oszlop a szilárdság oszlop mellett), válassza a szilárdságot Y-nak és a szállítót X-nek.
• A oldalon. 2. zóna, válassza ki az adatok típusát. Alapértelmezés szerint, ha az oszlop minőségi értékeket tartalmaz, az Ellistat csak az "Arány" típust fogja javasolni, de ha az adatok mennyiségiak, az Ellistat a két típust, az "arányt" és a "népességet" fogja javasolni. 📝: válassza a "népesség" lehetőséget.
• A oldalon. 3. zónaa 2. zónában kiválasztott grafikához.

• A 4. zóna. . a szignifikancia eredménye (a jobb oldalon jelenik meg) a különböző statisztikákkal együtt. (A két standard eltérés A és B közötti különbség akkor szignifikáns, ha a P-érték kisebb, mint 0,05. Az alábbi esetben megállapíthatjuk, hogy a különbség nem szignifikáns). 📝: A tartalom 4. zóna függ az adatok típusától, amelyet a 2. zóna.

Példa 3: Három vagy több standard eltérés összehasonlítása

Az Ellistat 2 tesztet kínál a standard eltérések összehasonlítására:

⇒A Bartlett-tesztkét vagy több standard eltérés összehasonlítása.

⇒A Levene-tesztkét vagy több standard eltérés összehasonlítása.

• Írja be a példa mennyiségi adatait a rácsba. A vizsgálat célja, hogy összehasonlítsa az A, B és C szállítók erősségeinek szórásait.
• Kattintson a "Következtetési statisztika" menüpontra.
• A 1. zónaVálassza ki az A, B és C oszlopokat Y-ban, ha az adatok 3 különböző oszlopban vannak. vagy ha az adatok egymásra vannak halmozva (egy szállítói oszlop az erősségeket tartalmazó oszlop mellett). válassza az erősséget Y-nak és a szállítót X-nek.
• A oldalon. 2. zóna, válassza ki az adatok típusát. Alapértelmezés szerint, ha az oszlop minőségi értékeket tartalmaz, az Ellistat csak az "Arány" típust fogja javasolni, de ha az adatok mennyiségiak, az Ellistat a két típust, az "arányt" és a "népességet" fogja javasolni. 📝: válassza a "népesség" lehetőséget.
• A oldalon. 3. zónaa 2. zónában kiválasztott grafikához.

• A 4. zóna. . a szignifikancia eredménye (a jobb oldalon jelenik meg) a különböző statisztikákkal együtt. (Az A, B és C standard eltérések közötti különbség akkor szignifikáns, ha a P-érték kisebb, mint 0,05. Az alábbi esetben megállapíthatjuk, hogy a különbség nem szignifikáns). 📝: A tartalom 4. zóna függ az adatok típusától, amelyet a 2. zóna.

3. Statisztikai tesztek a mediánok összehasonlítására

A mediánok összehasonlítása:

Az alábbi példák összefoglalják a mediánok összehasonlítására végzett összehasonlítások típusait.

Az alábbi linkek tartalmazzák az Ellistat Data Analysis által javasolt különböző medián-összehasonlító elemzésekhez használt adatokat. Vegyük példaként a következő adatokat:

Független adatok 🇺🇸/ Données indépendantes🇫🇷

Párosított adatok 🇺🇸/ Données appariées 🇫🇷

Ezen az adatkészleten számos elemzés végezhető.

Példa 1: Egy medián összehasonlítása egy elméleti értékkel :

Az Ellistat két nem parametrikus tesztet kínál a medián és az elméleti érték összehasonlítására.

⇒ Jelteszt

⇒ Wilcoxon-teszt

• Írja be a példa mennyiségi adatait a rácsba. A vizsgálat célja, hogy összehasonlítsuk az A szállító 5 N-os medián erejét.
• Kattintson a "Következtetési statisztika" menüpontra.
• A 1. zónaválassza ki a mennyiségi adatokat tartalmazó oszlopot Y-ban.
• A oldalon. 2. zóna, válassza ki az adatok típusát. Alapértelmezés szerint, ha az oszlop minőségi értékeket tartalmaz, az Ellistat csak az "Arány" típust fogja javasolni, de ha az adatok mennyiségiak, az Ellistat a két típust, az "arányt" és a "népességet" fogja javasolni. 📝: válassza a "népesség" lehetőséget.
• A oldalon. 3. zónaa 2. zónában kiválasztott grafikához.
• A 4. zónaA szignifikancia eredménye (a jobb oldalon látható) az alábbi különböző statisztikákkal együtt. (A medián és az elméleti érték közötti különbség akkor szignifikáns, ha a P-érték kisebb, mint 0,05. Az alábbi esetben megállapíthatjuk, hogy a különbség szignifikáns).

📝: A tartalom a 4. zóna függ az adatok típusától, amelyet a 2. zóna. A medián és az elméleti érték összehasonlításának megfelelő kiválasztásához válassza a nem parametrikus tesztet. lásd a következő ábrát.

💡 Kérjük, vegye figyelembe, hogy az Ellistat összes medián-összehasonlító tesztje nem parametrikus teszt, így az eredmények használatának nincsenek előfeltételei.

Példa 2: Két medián összehasonlítása.

Az Ellistat 3 tesztet kínál két különböző medián összehasonlítására.

⇒  Mann Withney teszt : a független adatok összehasonlítása esetén alkalmazva

⇒  Jelteszt : párosított adatokhoz igazítva

⇒  Wilcoxon-teszt: párosított adatokhoz igazítva

• Írja be a példa mennyiségi adatait a rácsba. A vizsgálat célja, hogy összehasonlítsa az A és a B szállító erősségének mediánját.
• Kattintson a "Következtetési statisztika" menüpontra.
• A 1. zónaHa az adatok 2 különböző oszlopban vannak, válassza ki az A és B oszlopot Y-ban. Ha az adatok egymásra vannak halmozva (egy szállító oszlop a szilárdság oszlop mellett), válassza a szilárdságot Y-nak és a szállítót X-nek.
• A oldalon. 2. zóna, válassza ki az adatok típusát. Alapértelmezés szerint, ha az oszlop minőségi értékeket tartalmaz, az Ellistat csak az "Arány" típust fogja javasolni, de ha az adatok mennyiségiak, az Ellistat a két típust, az "arányt" és a "népességet" fogja javasolni. 📝: válassza a "népesség" lehetőséget.
• A oldalon. 3. zónaa 2. zónában kiválasztott grafikához.

• A 4. zóna. . a szignifikancia eredménye (a jobb oldalon jelenik meg) a különböző statisztikákkal együtt. (A két A és B medián közötti különbség akkor szignifikáns, ha a P-érték kisebb, mint 0,05. Az alábbi esetben megállapíthatjuk, hogy a különbség nem szignifikáns).

📝: A tartalom a 4. zóna függ az adatok típusától, amelyet a 2. zóna. Két medián összehasonlításához válassza a nem parametrikus tesztet. lásd a következő ábrát.

💡 Kérjük, vegye figyelembe, hogy az Ellistat összes medián-összehasonlító tesztje nem parametrikus teszt. Tehát az eredmények kiaknázásához nincs szükség előfeltételre.

Példa 3: Három vagy több medián összehasonlítása .

Az Ellistat két nem parametrikus tesztet kínál három vagy több medián összehasonlítására.

⇒ Kruskal-Walis teszt : független adatokhoz igazítva

⇒ Friedman-teszt: az egyeztetett adatokhoz igazítva

• Írja be a példa mennyiségi adatait a rácsba. A vizsgálat célja az A, B és C szállítók erősségének mediánjainak összehasonlítása.
• Kattintson a "Következtetési statisztika" menüpontra.
• A 1. zónaVálassza ki az A, B és C oszlopokat Y-ban, ha az adatok 3 különböző oszlopban vannak. vagy ha az adatok egymásra vannak halmozva (egy szállítói oszlop az erősségeket tartalmazó oszlop mellett). válassza az erősséget Y-nak és a szállítót X-nek.
• A oldalon. 2. zóna, válassza ki az adatok típusát. Alapértelmezés szerint, ha az oszlop minőségi értékeket tartalmaz, az Ellistat csak az "Arány" típust fogja javasolni, de ha az adatok mennyiségiak, az Ellistat a két típust, az "arányt" és a "népességet" fogja javasolni. 📝: válassza a "népesség" lehetőséget.
• A oldalon. 3. zónaa 2. zónában kiválasztott grafikához.

• A 4. zóna. . a szignifikancia eredménye (a jobb oldalon jelenik meg) a különböző statisztikákkal együtt. (Az A, B és C mediánok közötti különbség akkor szignifikáns, ha a P-érték kisebb, mint 0,05. Az alábbi esetben megállapíthatjuk, hogy a különbség nem szignifikáns).

📝: A tartalom a 4. zóna függ az adatok típusától, amelyet a 2. zóna. Több medián összehasonlításához válassza a nem parametrikus tesztet. lásd a következő ábrát.

💡 Kérjük, vegye figyelembe, hogy az Ellistat összes medián-összehasonlító tesztje nem parametrikus teszt. Tehát az eredmények kiaknázásához nincs szükség előfeltételre.

Példa 4: Párosított adatok

A statisztikával összefüggésben a párosított adatok (vagy párosított adatok) olyan adathalmazokra utalnak, amelyekben a megfigyeléseket párban gyűjtik. Minden megfigyelési pár általában meghatározott módon kapcsolódik egymáshoz, lehetővé téve az egyes párokon belüli két érték közvetlen összehasonlítását.

Példa:

• Hasonlítsa össze a hőkezelés előtti és utáni középkeménységet.
• Hasonlítsa össze a fehérvérsejtszámot a kezelés előtt, az első adag kezelés után és a második adag kezelés után.

Párosított adatok mediánjainak összehasonlítása.

Az Ellistat 3 megfelelő tesztet kínál a párosított adatok mediánjainak összehasonlítására:

⇒⇒ Jelteszt : alkalmas két medián összehasonlítására.

⇒ Wilcoxon-teszt Két medián összehasonlításához.

⇒ Friedman-teszt: alkalmas 3 vagy több medián összehasonlítására

💡 Kérjük, vegye figyelembe, hogy az Ellistat összes medián-összehasonlító tesztje nem parametrikus teszt. Tehát az eredmények kiaknázásához nincs szükség előfeltételre.