Population

Ellistat Data Analysis offers a complete range of statistical testing parametric and non-parametric tests to compare a population of quantitative data. The purpose of these statistical tests is to compare two or more populations, either in terms of positions (such as means or medians) or variations (variances).

Hypothesis testing can be divided into two main categories:

• Parametric tests (in orange): These statistical tests make assumptions about the parameters of the population distribution, such as mean and variance, and include examples such as Student's t-test, ANOVA and the linear regression test.
• Non-parametric tests (green): These are statistical tests that make no assumptions about the distribution of population data, and include examples such as the Wilcoxon, Kruskal-Wallis or Friedman test.

The table below summarizes all the statistical tests available in Ellistat Data Analysis:

The following sections describe the statistical tests that can be performed with Ellistat Data Analysis:

1. Statistical tests for comparing averages

Comparison of averages:

The following examples summarize the types of comparisons made when comparing averages.

The links below contain the data used for the various mean-comparison analyses proposed by Ellistat Data Analysis. Let's take the following data as an example

Independent Data 🇺🇸/ Données indépendantes🇫🇷 

Paired Data 🇺🇸/ Données appariées 🇫🇷 

Example 1: Comparing an average with a theoretical value :

Perform a 1T test, to compare an average with a theoretical value.

• Enter the quantitative data from the example in the grid. The aim of this study is to compare the average force of supplier A with 5 N.
• Click on the "Inferential statistics" menu.
• In the zone 1Select the column with quantitative data in Y.
• In zone 2, choose your data type. By default, if the column contains qualitative values, Ellistat will propose "Proportion" only, but if the data is quantitative, Ellistat will propose both "proportion" and "population" types. 📝: choose "population".
• In zone 3to obtain the graphics selected in zone 2.
• In the zone 4The significance result (displayed on the right) with the various statistics below. (the difference between the mean and the theoretical value is significant if the P value is less than 0.05. In the following case, we can conclude that the difference is significant). 📝: The content of zone 4depends on the type of data selected in Zone 2.

Example 2: Comparing two averages

Perform a 2T test to compare two different averages.

• Put the quantitative data from the example in the grid. The aim of this study is to compare the average strengths of suppliers A and B.
• Click on the "Inferential statistics" menu.
• In the zone 1If the data is in 2 different columns, choose columns A and B in Y. If the data are stacked (a supplier column in addition to a strength column), choose strength as Y and supplier as X.
• In zone 2, choose your data type. By default, if the column contains qualitative values, Ellistat will propose "Proportion" only, but if the data is quantitative, Ellistat will propose both "proportion" and "population" types. 📝: choose "population".
• In zone 3to obtain the graphics selected in zone 2.

• In the zone 4. . the significance result (is displayed on the right) with the various statistics below. (the difference between the two means A and B is significant if the P value is less than 0.05. In the following case, we can conclude that the difference is not significant). 📝: The contents of zone 4 depends on the type of data selected in Zone 2.

Example 3: Compare three or more averages

Perform an ANOVA (Analysis of Variance) test, to compare 3 or more averages.

• Enter the quantitative data from the example in the grid. The aim of this study is to compare the average strengths of suppliers A, B and C.
• Click on the "Inferential statistics" menu.
• In the zone 1Choose columns A, B and C in Y if the data are in 3 different columns. or if the data are stacked (a supplier column in addition to a strength column). choose strength as Y and supplier as X.
• In zone 2, choose your data type. By default, if the column contains qualitative values, Ellistat will propose "Proportion" only, but if the data is quantitative, Ellistat will propose both "proportion" and "population" types. 📝: choose "population".
• In zone 3to obtain the graphics selected in zone 2.

• In the zone 4. . the significance result (is displayed on the right) with the various statistics below. (the difference between means A, B and C is significant if the P value is less than 0.05. In the following case, we can conclude that the difference is not significant). 📝: The content of zone 4 depends on the type of data selected in Zone 2.

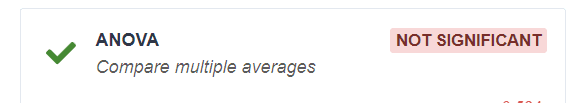
Example 4: Paired data

In the context of statistics, paired data (or matched data) refers to data sets where observations are collected in pairs. Each pair of observations is usually linked in a specific way, enabling direct comparison of the two values within each pair.

Example:

• Compare average hardness before and after heat treatment.
• Compare white blood cell counts before, after the first dose of treatment and after the second dose of treatment.

To compare the means of paired data.

Ellistat offers two suitable tests for comparing the means of paired data:

⇒ T-test for paired data for two averages.

⇒ ANOVA for paired data for two or more averages.

Paired Data 🇺🇸/ Données appariées 🇫🇷 

2. Statistical tests to compare standard deviations

Comparison of standard deviations:

The following examples summarize the types of comparisons made to compare standard deviations.

The links below contain the data used for the various standard deviation analyses proposed by Ellistat Data Analysis. Let's take the following data as an example:

Independent Data 🇺🇸/ Données indépendantes🇫🇷 

Example 1: Comparing a standard deviation with a theoretical value :

Create a Chi-2 testto compare a standard deviation with a theoretical value.

• Enter the quantitative data from the example in the grid. The objective of this study is to compare the standard deviation of the force of supplier A with 1 N.
• Click on the "Inferential statistics" menu.
• In the zone 1Select the column with quantitative data in Y.
• In zone 2, choose your data type. By default, if the column contains qualitative values, Ellistat will propose "Proportion" only, but if the data is quantitative, Ellistat will propose both "proportion" and "population" types. 📝: choose "population".
• In zone 3to obtain the graphics selected in zone 2.
• In the zone 4Put in the theoretical value . the significance result (is displayed on the right) with the different statistics below. (the difference between the standard deviation and the theoretical value is significant if the P value is less than 0.05. In the following case, we can conclude that the deviation is significant). 📝: The content of zone 4depends on the type of data selected in Zone 2.

Example 2: Comparing two standard deviations.

Ellistat offers 2 tests to compare standard deviations:

⇒Fischer testto compare two different standard deviations.

⇒The Levene testto compare two or more standard deviations.

• Put the quantitative data from the example in the grid. The aim of this study is to compare the standard deviations of the strengths of suppliers A and B.
• Click on the "Inferential statistics" menu.
• In the zone 1If the data is in 2 different columns, choose columns A and B in Y. If the data are stacked (a supplier column in addition to a strength column), choose strength as Y and supplier as X.
• In zone 2, choose your data type. By default, if the column contains qualitative values, Ellistat will propose "Proportion" only, but if the data is quantitative, Ellistat will propose both "proportion" and "population" types. 📝: choose "population".
• In zone 3to obtain the graphics selected in zone 2.

• In the zone 4. . the significance result (is displayed on the right) with the various statistics below. (The difference between the two standard deviations A and B is significant if the P value is less than 0.05. In the following case, we can conclude that the difference is not significant). 📝: The content of zone 4 depends on the type of data selected in Zone 2.

Example 3: Comparing three or more standard deviations

Ellistat offers 2 tests to compare standard deviations:

⇒The Bartlett testto compare two or more standard deviations.

⇒The Levene testto compare two or more standard deviations.

• Put the quantitative data from the example in the grid. The aim of this study is to compare the standard deviations of the strengths of suppliers A, B and C.
• Click on the "Inferential statistics" menu.
• In the zone 1Choose columns A, B and C in Y if the data are in 3 different columns. or if the data are stacked (a supplier column in addition to a strength column). choose strength as Y and supplier as X.
• In zone 2, choose your data type. By default, if the column contains qualitative values, Ellistat will propose "Proportion" only, but if the data is quantitative, Ellistat will propose both "proportion" and "population" types. 📝: choose "population".
• In zone 3to obtain the graphics selected in zone 2.

• In the zone 4. . the significance result (is displayed on the right) with the various statistics below. (the difference between the A, B and C standard deviations is significant if the P value is less than 0.05. In the following case, we can conclude that the difference is not significant). 📝: The content of zone 4 depends on the type of data selected in Zone 2.

3. Statistical tests for comparing medians

Comparison of medians:

The following examples summarize the types of comparisons made when comparing medians.

The links below contain the data used for the different median comparison analyses proposed by Ellistat Data Analysis. Let's take the following data as an example:

Independent Data 🇺🇸/ Données indépendantes🇫🇷

Paired Data 🇺🇸/ Données appariées 🇫🇷

Several analyses can be performed on this dataset.

Example 1: Comparing a median with a theoretical value :

Ellistat offers two non-parametric tests to compare the median with a theoretical value.

⇒ Sign test

⇒ Wilcoxon test

• Put in the quantitative data grid of the example. The aim of this study is to compare the Median force of supplier A with 5 N.
• Click on the "Inferential statistics" menu.
• In the zone 1Select the column with quantitative data in Y.
• In zone 2, choose your data type. By default, if the column contains qualitative values, Ellistat will propose "Proportion" only, but if the data is quantitative, Ellistat will propose both "proportion" and "population" types. 📝: choose "population".
• In zone 3to obtain the graphics selected in zone 2.
• In the zone 4The significance result (displayed on the right) with the various statistics below. (the difference between the median and the theoretical value is significant if the P value is less than 0.05. In the following case, we can conclude that the difference is significant).

📝: The contents of zone 4 depends on the type of data selected in Zone 2. To properly select the comparison of a median with a theoretical value, choose the non-parametric test. see following figure.

💡 Please note that all median comparison tests in Ellistat are non-parametric, so no prerequisites are required to use the results.

Example 2: Compare two medians.

Ellistat offers 3 tests to compare two different medians.

⇒  Mann Withney Test: dapted for comparison of independent data

⇒  Sign test : adapted for matched data

⇒  Wilcoxon test: adapted for matched data

• Put the quantitative data from the example in the grid. The aim of this study is to compare the medians of the strengths of suppliers A and B.
• Click on the "Inferential statistics" menu.
• In the zone 1If the data is in 2 different columns, choose columns A and B in Y. If the data are stacked (a supplier column in addition to a strength column), choose strength as Y and supplier as X.
• In zone 2, choose your data type. By default, if the column contains qualitative values, Ellistat will propose "Proportion" only, but if the data is quantitative, Ellistat will propose both "proportion" and "population" types. 📝: choose "population".
• In zone 3to obtain the graphics selected in zone 2.

• In the zone 4. . the significance result (is displayed on the right) with the various statistics below. (The difference between the two medians A and B is significant if the P value is less than 0.05. In the following case, we can conclude that the difference is not significant).

📝: The contents of zone 4 depends on the type of data selected in Zone 2. To select the comparison of two medians, choose the non-parametric test. see next figure.

💡 Please note that all median comparison tests in Ellistat are non-parametric. So no prerequisite is required to exploit the results.

Example 3: Compare three or more medians .

Ellistat offers two non-parametric tests to compare three or more medians.

⇒ Kruskal-Walis test : adapted to independent data

⇒ Friedman test: adapted to matched data

• Put the quantitative data from the example in the grid. The aim of this study is to compare the medians of the strengths of suppliers A, B and C.
• Click on the "Inferential statistics" menu.
• In the zone 1Choose columns A, B and C in Y if the data are in 3 different columns. or if the data are stacked (a supplier column in addition to a strength column). choose strength as Y and supplier as X.
• In zone 2, choose your data type. By default, if the column contains qualitative values, Ellistat will propose "Proportion" only, but if the data is quantitative, Ellistat will propose both "proportion" and "population" types. 📝: choose "population".
• In zone 3to obtain the graphics selected in zone 2.

• In the zone 4. . the significance result (is displayed on the right) with the various statistics below. (the difference between the medians A, B and C is significant if the P value is less than 0.05. In the following case, we can conclude that the difference is not significant).

📝: The contents of zone 4 depends on the type of data selected in Zone 2. To select the comparison of several medians, choose the non-parametric test. see next figure.

💡 Please note that all median comparison tests in Ellistat are non-parametric tests. So no prerequisite is required to exploit the results.

Example 4: Paired data

In the context of statistics, paired data (or matched data) refers to data sets where observations are collected in pairs. Each pair of observations is usually linked in a specific way, enabling direct comparison of the two values within each pair.

Example:

• Compare median hardness before and after heat treatment.
• Compare white blood cell counts before, after the first dose of treatment and after the second dose of treatment.

To compare the medians of paired data.

Ellistat offers 3 suitable tests for comparing the medians of paired data:

⇒⇒ Sign test : suitable for comparing two medians.

⇒ Wilcoxon test suitable for comparing two medians.

⇒ Friedman test: suitable for comparing 3 or more medians

💡 Please note that all the median comparison tests in Ellistat are non-parametric tests. No prerequisite is therefore required to exploit the results.