Il disegno degli esperimenti di Taguchi è un metodo statistico utilizzato per migliorare la qualità dei prodotti e dei processi produttivi. Sviluppato dal Dr. Genichi Taguchi L'obiettivo di questo piano è identificare i fattori che hanno la maggiore influenza sulla variazione di un prodotto o di un processo, riducendo al minimo il numero di esperimenti necessari.
Questo metodo organizza gli esperimenti in modo sistematico ed efficiente, consentendo di analizzare contemporaneamente gli effetti di diverse variabili. L'obiettivo principale è quello di rendere il prodotto o il processo robusto contro le variazioni esterne e interne, garantendo così prestazioni stabili e di alta qualità.
Costruire un disegno sperimentale - Metodo Taguchi
Definizione dei fattori e dei livelli
La definizione dei fattori implica la scelta dei fattori da studiare. Per scegliere i fattori giusti, si consiglia di comprendere innanzitutto il processo o il prodotto in questione, quindi di eseguire le seguenti operazioni:
- Organizzare sessioni di brainstorming con un team multidisciplinare per generare un elenco esaustivo di potenziali fattori.
- Valutare l'importanza di ciascun fattore in termini di impatto potenziale sul risultato finale. Dare priorità ai fattori che possono avere un effetto significativo.
- Selezionate i fattori rilevanti per il disegno sperimentale in base all'importanza del fattore, alla vostra capacità di controllarlo e alla facilità di misurarlo in modo affidabile.
Per ogni fattore individuato, occorre poi definire i livelli studiati. È importante scegliere livelli pertinenti:
- Larghezza della spiaggia Selezionare livelli che coprano un intervallo sufficientemente ampio per rilevare gli effetti dei fattori, ma senza arrivare a estremi non realistici che potrebbero essere inutili o pericolosi.
- Pratico Assicurare che i livelli scelti siano raggiungibili in un contesto produttivo reale.
Scelta del tavolo
Una volta identificati i fattori, è necessario creare il disegno sperimentale. A questo scopo, si consiglia di usare il modulo di analisi dei dati Ellistat che dispone di un esclusivo motore di progettazione di esperimenti. È in grado di trovare un disegno con la migliore strategia possibile data una determinata strutturazione delle interazioni. Le tabelle programmate in Ellistat sono L4, L8, L12, L16, L20 e L32.
Ecco gli elementi da tenere in considerazione quando si crea un disegno sperimentale con la metodologia di Taguchi:
Nozione di interazione
L'interazione A*B si riferisce al fatto che il livello di A influenza l'effetto di B e viceversa.
Esempio:
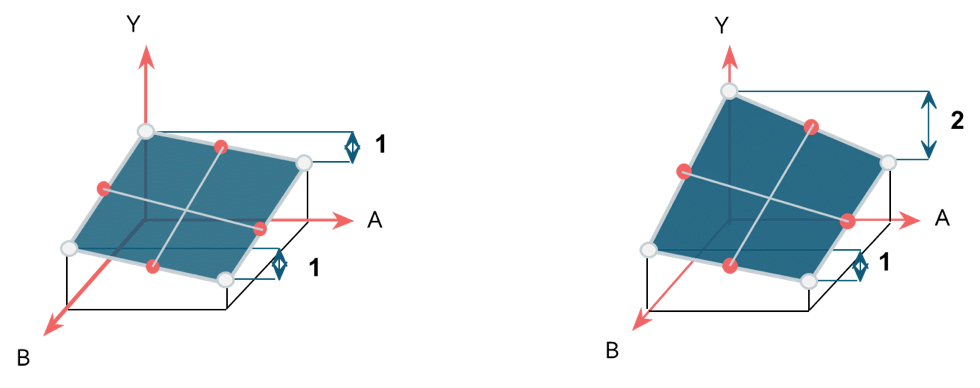
Nell'esempio precedente, la figura a sinistra mostra :
Qualunque sia il livello del fattore B, l'effetto di A sulla Y è lo stesso e A ha un effetto di 1 sulla risposta. Non c'è quindi alcuna interazione tra A e B.
La figura a destra mostra :
Quando il livello del fattore B è minimo, l'effetto di A sulla Y è pari a 2. Quando il livello del fattore B è massimo, l'effetto di A sulla Y è pari a 1. L'effetto di A varia in funzione del livello di B. Esiste pertanto un'interazione tra A e B.
Quando c'è un'interazione, l'effetto dell'interazione è modellato da un termine moltiplicativo nell'equazione di previsione Y, in questo caso A*B.
La forma dell'equazione di previsione sarebbe :
Y=\alpha_0+\alpha_1*A+\alpha_2*B+\alpha_3*A*B
Il termine α3 corrisponde all'interazione A*B
Nozione di alias
Il termine alias tra due fattori si riferisce al fatto che i fattori hanno lo stesso livello per tutti gli esperimenti del disegno sperimentale.
Ad esempio, supponiamo di aver realizzato il seguente disegno sperimentale:
| A | B | Y |
|---|---|---|
| 1 | 1 | 5 |
| 1 | 1 | 5 |
| 2 | 2 | 10 |
| 2 | 2 | 10 |
I fattori A e B variano contemporaneamente, quindi non è possibile distinguere il fattore A dal fattore B, né dire quale dei due fa variare la Y da 5 a 10 quando passa da 1 a 2. Diremo che questi due fattori sono alias.
Ovviamente, quando si costruisce un disegno sperimentale, si scelgono con cura le prove in modo che nessun fattore sia alias con un altro fattore. Tuttavia, è possibile che un fattore sia alias con un'interazione. Prendiamo il seguente esempio:
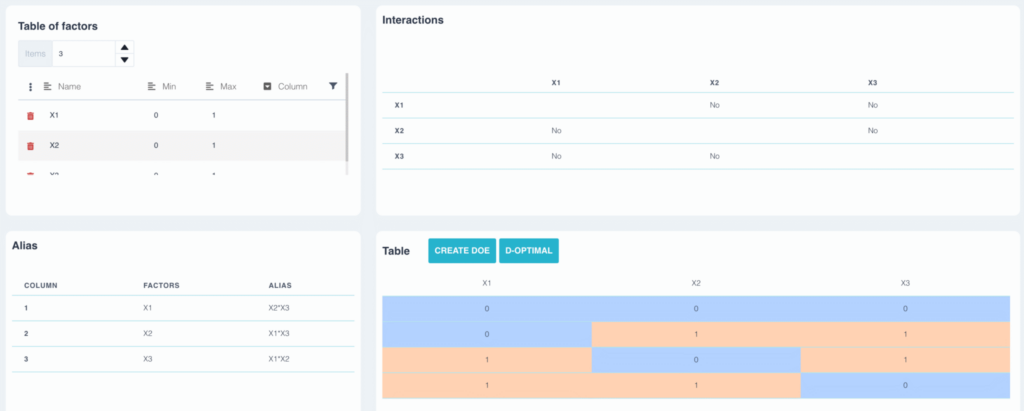
In questo esempio, abbiamo costruito un piano a tre fattori utilizzando la tabella L4. La tabella degli alias mostra :
- Il fattore a viene aliasato con l'interazione b*c
- Il fattore b è alias con l'interazione a*c
- Il fattore c è alias con l'interazione a*b
Allo stesso modo, se due fattori sono alias, non sarà possibile dire alla fine del disegno sperimentale se l'effetto osservato è dovuto al fattore a, all'interazione bc o la somma delle due. Assumeremo quindi che l'interazione bc è pari a zero, ma ciò resta da verificare sperimentalmente.
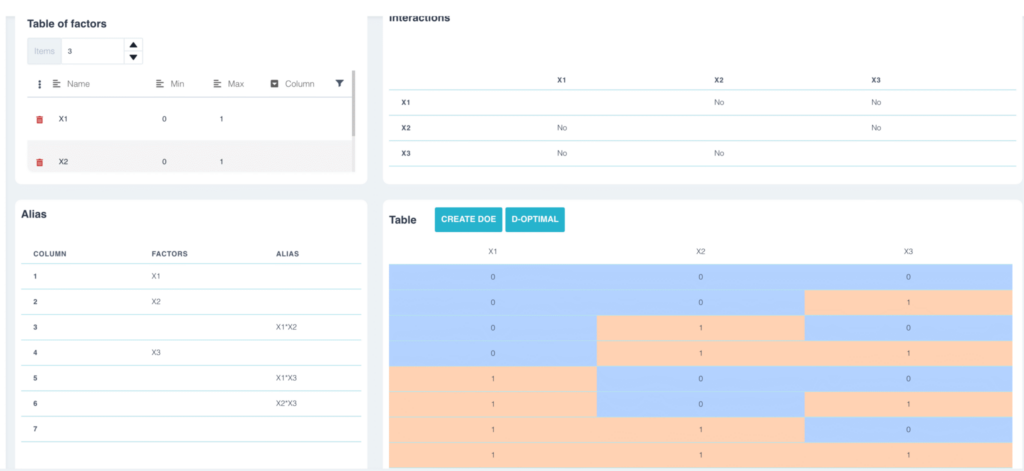
Per evitare questo tipo di problema, in genere si scelgono disegni sperimentali in cui nessuno dei fattori è alias con un'interazione. Nell'esempio precedente avremmo potuto scegliere un disegno L8 in cui nessuno dei fattori è alias con un'interazione.
Risolvere un disegno sperimentale
La risoluzione di un disegno di esperimento corrisponde al livello di alias di questo disegno.
Risoluzione III
Un disegno sperimentale è di risoluzione III se almeno un fattore (ordine I) è alias con un'interazione di tipo A*B (ordine II).
Questo tipo di disegno riduce notevolmente il numero di prove, ma presuppone che tutte le interazioni siano nulle. Occorre prestare attenzione nell'interpretazione dei risultati e l'ipotesi di interazioni nulle deve essere convalidata da ulteriori prove.
Esempio:
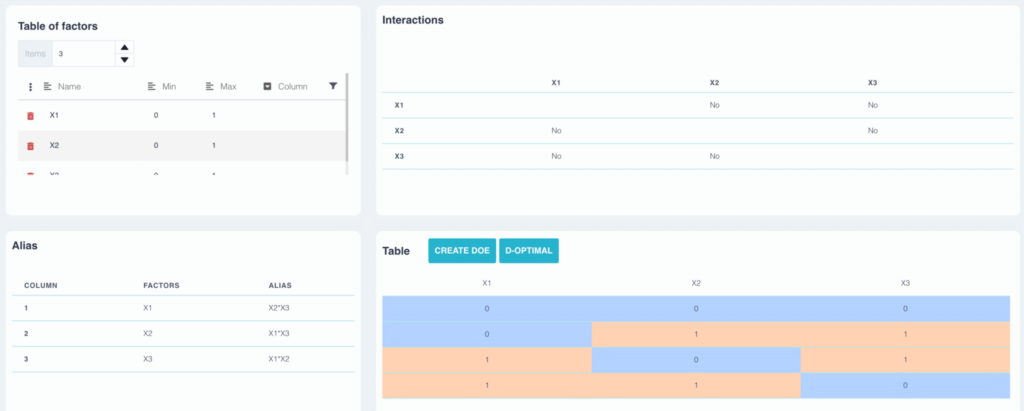
Nel disegno precedente, il fattore a è alias con l'interazione b*c. Il disegno è la risoluzione III
Risoluzione IV
Un disegno sperimentale è di risoluzione IV se :
- Nessun fattore è alias con un'interazione (ordine II)
- Almeno un'interazione (ordine II) è alias con un'altra interazione (ordine II)
Questo tipo di disegno limita il numero di prove. Presuppone che la maggior parte delle interazioni sia nulla, tranne alcune che possono essere identificate. Questo è generalmente il caso.
Dato che i fattori non sono allineati con altre interazioni, l'effetto di tutti i fattori può essere calcolato in modo inequivocabile.
Questo è il tipo di piano più utilizzato.
Esempio:
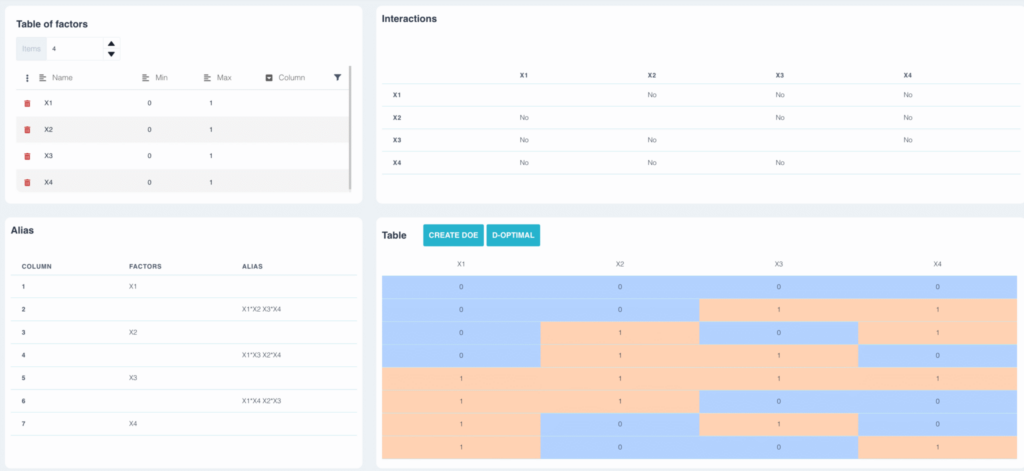
Nel piano precedente, nessuno dei fattori è associato a un'altra interazione. Le interazioni ab e cd sono alias, quindi il piano è la risoluzione IV.
Risoluzione V
Un disegno sperimentale è di risoluzione IV se :
- Nessun fattore è alias con un'interazione (ordine II)
- Questa tipologia di disegno limita il numero di prove rispetto al disegno completo.
Dato che i fattori non sono allineati con altre interazioni, l'effetto di tutti i fattori può essere calcolato in modo inequivocabile.
Dal momento che le interazioni non sono alias con altre interazioni, l'effetto di tutte le interazioni può essere calcolato in modo inequivocabile.
Questo è il tipo di piano ideale, ma purtroppo ne esiste solo uno con meno di 20 prove. Si tratta di un piano a 5 fattori che utilizza la tabella L16.


