Taguchi's experimental design is a statistical method used to improve the quality of products and manufacturing processes. Developed by the Dr. Genichi Taguchi The aim of this plan is to identify the most influential factors in the variation of a product or process, while minimizing the number of experiments required.
This method organizes experiments systematically and efficiently, enabling the effects of several variables to be analyzed simultaneously. The main objective is to make the product or process robust against external and internal variations, thus ensuring stable, high-quality performance.
Building an experimental design - Taguchi method
Defining factors and levels
Defining the factors involves selecting the factors to be studied. To select the right factors, we recommend that you first understand the process or product concerned, and then carry out the following steps:
- Organize brainstorming sessions with a multidisciplinary team to generate an exhaustive list of potential factors.
- Assess the importance of each factor in terms of its potential impact on the final result. Prioritize factors likely to have a significant effect.
- Select the factors relevant to the experimental design according to the importance of the factor, your ability to control it, and the ease of measuring it reliably.
For each factor identified, we then need to define the levels studied. It is important to choose the right levels:
- Beach width Select levels that cover a sufficiently wide range to detect the effects of factors, but without going to unrealistic extremes that could be unnecessary or dangerous.
- Practical To ensure that the levels selected are achievable in a real-life production context.
Table selection
Once the factors have been identified, you need to create the experimental design. To do this, we recommend using Ellistat's Data Analysis module which features an exclusive experiment design engine. It is capable of finding a design with the best possible strategy given a given structuring of interactions. The tables programmed in Ellistat are L4, L8, L12, L16, L20 and L32.
Here are the elements to take into account when creating your experimental design according to Taguchi's methodology:
Notion of interaction
A*B interaction refers to the fact that the level of A influences the effect of B, and vice versa.
Example:
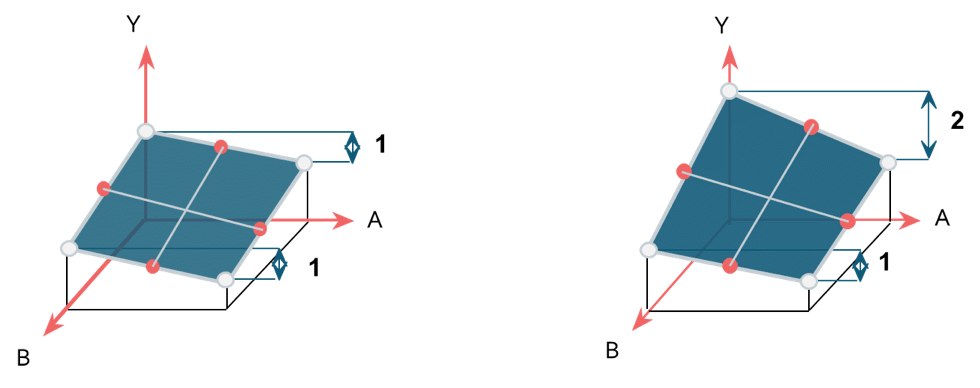
In the previous example, the figure on the left shows :
Whatever the level of factor B, the effect of A on Y is the same, and A has an effect of 1 on the response. There is therefore no interaction between A and B.
The figure on the right shows :
When the level of factor B is at a minimum, the effect of A on the Y is 2. When the level of factor B is at a maximum, the effect of A on the Y is 1. The effect of A varies according to the level of B. There is therefore an interaction between A and B.
When there is an interaction, we model the effect of the interaction by a multiplicative term in the Y prediction equation, here A*B.
The form of the forecasting equation would be :
Y=\alpha_0+\alpha_1*A+\alpha_2*B+\alpha_3*A*B
The term α3 corresponds to the A*B interaction
Notion of alias
An alias between two factors means that the factors have the same level for all experiments in the experimental design.
For example, let's suppose we've carried out the following experimental design:
| A | B | Y |
|---|---|---|
| 1 | 1 | 5 |
| 1 | 1 | 5 |
| 2 | 2 | 10 |
| 2 | 2 | 10 |
Factors A and B vary at the same time, so it's not possible to differentiate factor A from factor B, or to say which of the two causes the Y to change from 5 to 10 when it goes from 1 to 2. We'll say that these two factors are aliases.
Obviously, when constructing an experimental design, you choose your trials carefully so that no factor is aliased to another factor. However, it is possible for a factor to be aliased with an interaction. Take the following example:
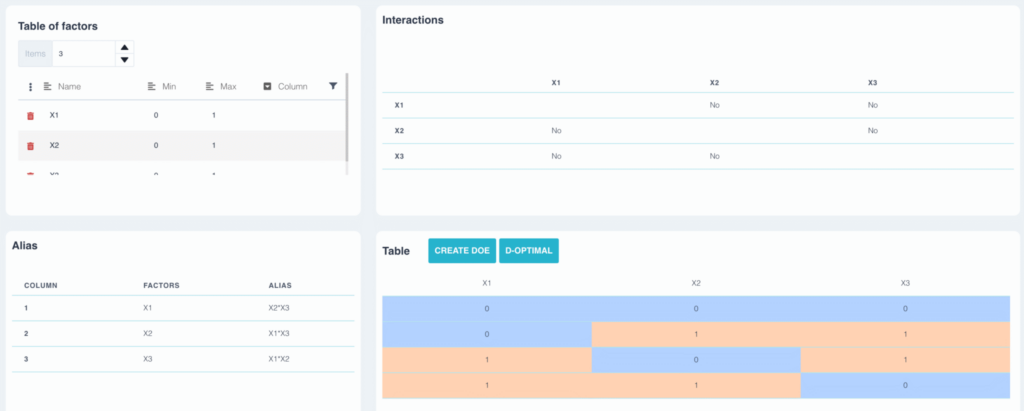
In this example, we've built a three-factor plan using table L4. The alias table shows :
- Factor a is aliased with interaction b*c
- Factor b is aliased with interaction a*c
- Factor c is aliased with interaction a*b
In the same way, if two factors are aliased, it will not be possible to say at the end of the experimental design whether the effect observed is due to factor a, to interaction bc or the sum of the two. We therefore assume that the interaction bc is zero, but this remains to be verified experimentally.
To avoid this type of problem, we generally choose experimental designs in which none of the factors are aliased with an interaction. In the previous example, we could have chosen an L8 design in which none of the factors is aliased with an interaction.
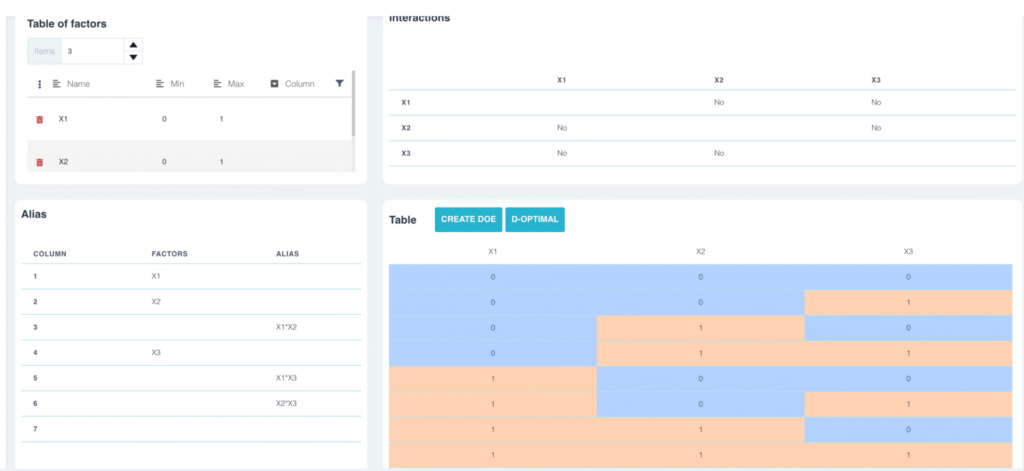
Solving a design of experiment
The resolution of an experimental design corresponds to its alias level.
Resolution III
An experimental design is of resolution III if at least one factor (order I) is aliased with a type A*B interaction (order II).
This type of design greatly reduces the number of trials, but assumes that all interactions are zero. Care must be taken when interpreting the results, and the hypothesis of zero interactions must be validated by additional trials.
Example:
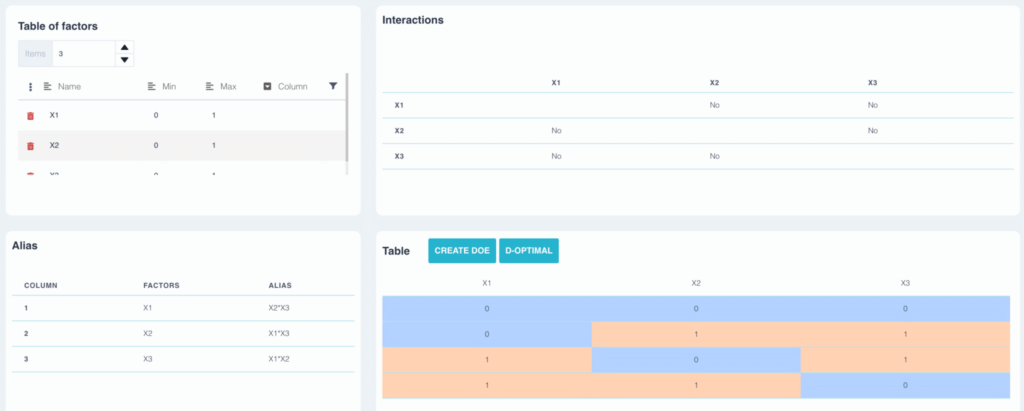
In the previous plan, factor a is aliased with interaction b*c. The plane is resolution III
Resolution IV
An experimental design is of resolution IV if :
- No factor is aliased with an interaction (order II)
- At least one interaction (order II) is aliased with another interaction (order II)
This type of design limits the number of trials. It assumes that the majority of interactions are zero, except for a few that can be identified. This is generally the case.
As the factors are not aliased with other interactions, we can unambiguously calculate the effect of all the factors.
This is the type of plan most often used.
Example:
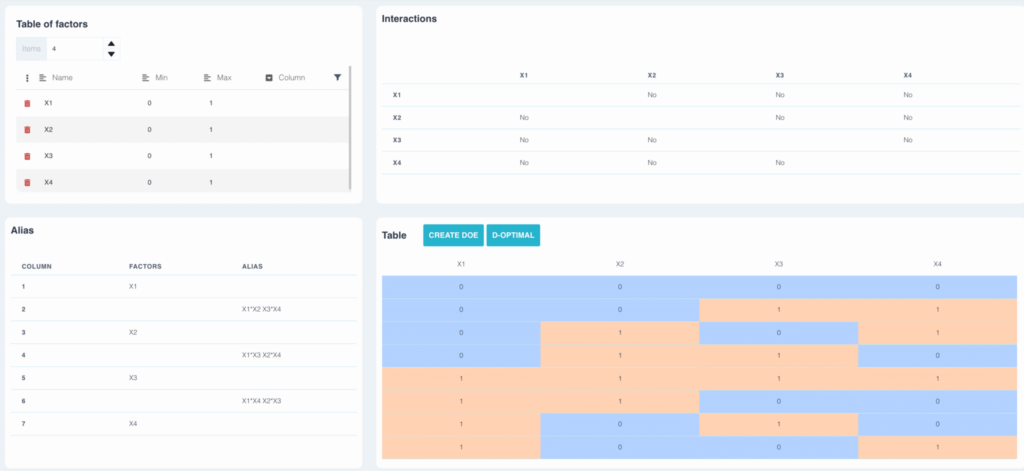
In the previous plan, none of the factors is aliased with another interaction. The interactions ab and cd are aliased, so the plan is resolution IV.
Resolution V
An experimental design is of resolution IV if :
- No factor is aliased with an interaction (order II)
- No interaction (order II) is aliased with another interaction (order II) This type of design limits the number of trials compared with the complete design.
As the factors are not aliased with other interactions, we can unambiguously calculate the effect of all the factors.
Since interactions are not aliased with other interactions, the effect of all interactions can be calculated unambiguously.
This is the ideal type of plan, but unfortunately there's only one with fewer than 20 trials. It's a 5-factor plan using the L16 table.


