Pour tester la normalité, il existe plusieurs tests qui permettent de valider ou non l’hypothèse selon laquelle la répartition des pièces suit une loi normale. Les tests habituellement utilisés sont :
- Le test de Khi2
- Le test d’Anderson-Darling
Test de normalité avec le test de Chi2
Pour vérifier la normalité d’une distribution, notre première intuition serait de tracer l’histogramme de la répartition des variables observées. Puis, de comparer si cet histogramme ressemble peu ou prou à la courbe de Gauss habituelle.
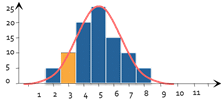
C’est exactement le principe du test du Chi2. Il ajoute à cette intuition une petite dose de calcul statistique. Le principe est le suivant :
d_i=\frac{(N_i-NP_i)^{2}}{NP_i}
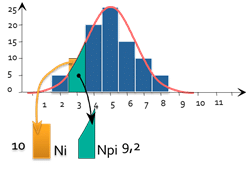
Pour chaque barre de l’histogramme, on peut calculer :
- Ni : Le nombre de pièces effectivement observées (ici 10)
- Npi : Le nombre de pièces théoriquement observées si la loi était normale (ici 9.2)
- di représente le « nombre de pièces mal rangées »
On calcule ensuite
D=\sum_{}^{}D_i
et il se trouve que D suit une loi de répartition du à n-2 degrés de liberté (N étant le nombre de classes). Par suite, on peut calculer la probabilité d’obtenir une telle valeur.
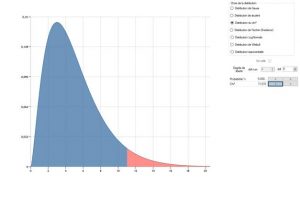
Par exemple, pour un histogramme comportant 7 classes, si nous avons calculé un D de 11.07, on calcule qu’il y a 5% d’obtenir une telle valeur ou plus si la loi de répartition des pièces est effectivement normale.
Le résultat du test sera donc 5% et on conclut en général de la manière suivante :
- Si X < 5% : la loi de distribution des variables n’est pas considérée comme suivant une loi normale.
- Si X >= 5% : l’hypothèse de normalité est acceptée, on peut considérer que la loi de distribution suit une loi normale.
Que faire en cas de non normalité
Le théorème central limite nous indique :
Tout système, résultant de la somme de nombreux facteurs indépendants les uns des autres et d’un ordre de grandeur équivalent, génère une loi de répartition qui tend vers une loi normale.
Mais on peut également raisonner de la manière inverse. Si l’on observe une loi qui n’est pas normale alors l’une des hypothèses du théorème n’est pas valide :
- Cas 1 : le système n’est pas résultant de la somme de nombreux facteurs : Il est peut-être le produit de nombreux facteurs ou autre. Dans ce cas, la loi de distribution peut être différente et en générale une transformation (en prenant par exemple le log du résultat) permettra de retrouver une loi normale.
- Cas 2 : Les facteurs ne sont pas indépendants les uns des autres
- Cas 3 : Les facteurs ne sont pas d’un ordre de grandeur équivalent :
- Un facteur est prépondérant devant les autres. Dans ce cas, il convient de trouver le facteur en question car lui seul génère une source importante de variabilité.
- Une valeur aberrante pollue la distribution. Dans ce cas, il convient de trouver la cause de la valeur aberrante et de l’éliminer si la cause a pu être expliquée.
Dans ces deux cas de figure, il ne faut pas trouver une loi de distribution correspondant à la variabilité observée. En effet, cette loi de distribution ne sera pas répétable dans le temps car due à un seul paramètre, elle n’aura donc aucune propriété prédictive.
Si l’origine de la non normalité est due au cas 1, il convient dès lors de trouver la loi de distribution correspondante, en particulier si l’on souhaite prédire le pourcentage de valeurs en dehors de la tolérance. Pour cela vous pouvez utiliser les propositions de lois de distribution situées en bas de la fenêtre dans le module Data Analysis pour voir si l’une des distributions permet de rendre compte des données observées :

