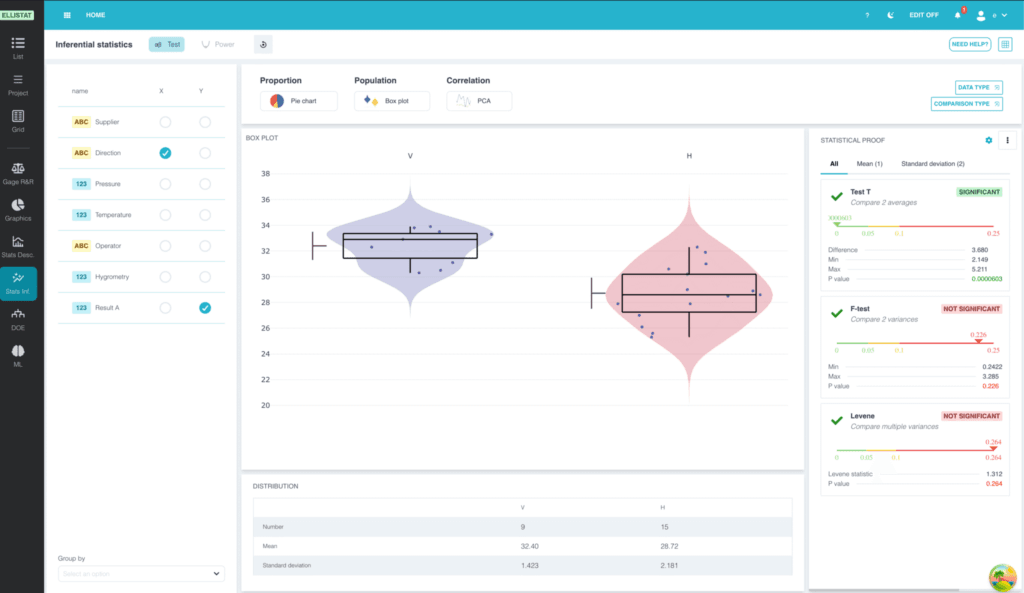
Avant de rentrer dans le détail des tests paramétriques et non paramétrique, rappelons le fonctionnement d’un test statistique. Le module Data Analysis d’Ellistat vous permet réaliser ces tests.
Un test statistique fonctionne de la manière suivante :
- On considère une hypothèse nulle dans laquelle il n’y a pas de différence entre les échantillons.
- On calcule la probabilité de tomber dans la même configuration que celle obtenue avec les échantillons observés en suivant l’hypothèse nulle. On appelle cette probabilité « Risque alpha » ou « p-value ».
- Si risque alpha < 5%, on considère qu’il est trop peu probable d’obtenir une telle configuration dans le cadre de l’hypothèse nulle. On rejette donc l’hypothèse nulle et on considère que la différence entre les échantillons est significative. Pour cette raison tous les résultats des tests statistiques proposés par Ellistat se trouveront associés à une valeur de risque alpha avec l’échelle suivante :
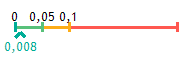
Le chiffre inscrit en dessous de l’échelle est égal au risque alpha du test :
- Si risque alpha < 0.01, la différence sera considérée comme très significative<
- Si risque alpha < 0.05, la différence sera considérée comme significative
- Si risque alpha < 0.1, la différence sera considérée comme limite. (On ne peut pas affirmer qu’il y a une différence significative mais l’hypothèse est intéressante)
- Si risque alpha > 0.1, la différence sera considérée comme non significative
Exemple
Pour illustrer le fonctionnement d’un test statistique prenons l’exemple suivant.
Supposons que l’on souhaite détecter le fait qu’une pièce soit pipée et la tirant à pile ou face. Nous supposons que la pièce tombe toujours sur pile.
Lancer n°1
Après le premier lancer, la pièce tombe sur pile, peut-on pour autant en déduire que la pièce est pipée ?
A priori, ce serait assez osé de parier que la pièce est pipée, car cela aurait très bien pu arriver avec une pièce standard.
Dans ce cas, l’hypothèse nulle est : la pièce n’est pas pipée, elle a donc une chance sur deux de tomber sur pile ou face. La probabilité qu’une pièce non pipée tombe sur pile est de 50%.
Par suite, la probabilité d’obtenir pile après le premier lancer d’une pièce non pipée est de 50%, on dira que le risque alpha du test est :Risque alpha = 50%
C’est-à-dire, il y a 50% de chance d’obtenir le même résultat en suivant l’hypothèse nulle.
Lancer n°2
Après le deuxième lancer, la pièce tombe à nouveau sur pile. Le risque alpha devient :Risque alpha = 25%
Peut-on pour autant en déduire que la pièce est pipée ?
Se pose ainsi la question : à partir de quel risque alpha peut-on dire que la pièce est pipée?
En règle générale, dans l’industrie, le risque alpha limite est choisi à 5%.
C’est-à-dire :
- Si risque alpha < 5%, on rejette l’hypothèse nulle et on considère que la pièce est pipée.
- Si risque alpha > 5%, on ne peut pas affirmer que la pièce est pipée. Cela ne signifie pas pour autant que la pièce n’est pas pipée car cela dépend du nombre de lancer que l’on a fait.
Suite de l’exemple
Poursuivons notre exemple :
-3ème lancer, la pièce tombe sur pile : Risque alpha = 12.5%
-4ème lancer, la pièce tombe sur pile : Risque alpha = 6.75%
-5ème lancer, la pièce tombe sur pile : Risque alpha = 3.375%
Dans ce cas, à partir du 5ème lancer de suite sur laquelle la pièce tombe sur pile, on peut donc affirmer que la pièce est pipée avec une risque inférieur à 5%.
Tests paramétriques vs non paramétriques
Lorsque l’on réalise des comparaisons de population ou que l’on compare une population à une valeur théorique, il existe deux grandes familles de tests : les tests paramétriques, et les tests non paramétriques.
Tests paramétriques
Les tests paramétriques fonctionnent en supposant que les données que l’on a à disposition suivent un type de loi de distribution connu (en général la loi normale).
Pour calculer le risque alpha du test statistique, il suffit de calculer la moyenne et l’écart-type de l’échantillon afin d’accéder à la loi de distribution de l’échantillon.
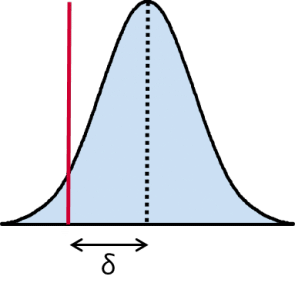
La loi de distribution étant ainsi parfaitement connue, on peut calculer le risque alpha en se basant sur les calculs théoriques de la loi gaussienne.
Ces tests sont en général très fins, mais ils nécessitent que les données suivent effectivement la loi de distribution supposée. Ils sont en particulier très sensibles aux valeurs aberrantes et ne sont pas conseillés si des valeurs aberrantes sont détectées.
Tests non paramétriques
Les tests non paramétriques ne font aucune hypothèse sur le type de loi de distribution des données. Ils se basent uniquement sur les propriétés numériques des échantillons. Voici un exemple de test non paramétrique :
On souhaite vérifier que la médiane d’une population est différente d’une valeur théorique. On mesure 14 pièces et on obtient l’échantillon suivant :

11 fois du même coté sur 14
11 fois sur 14, le résultat est inférieur à la médiane théorique. Si la médiane de la population est égale à la valeur théorique, on devrait avoir 50% des pièces supérieures à la médiane et 50% des pièces inférieures. Pour statuer sur la significativité de l’écart de la médiane à la médiane théorique, il suffit donc de vérifier si la fréquence de 11 fois sur 14 est significativement différente de 50%.
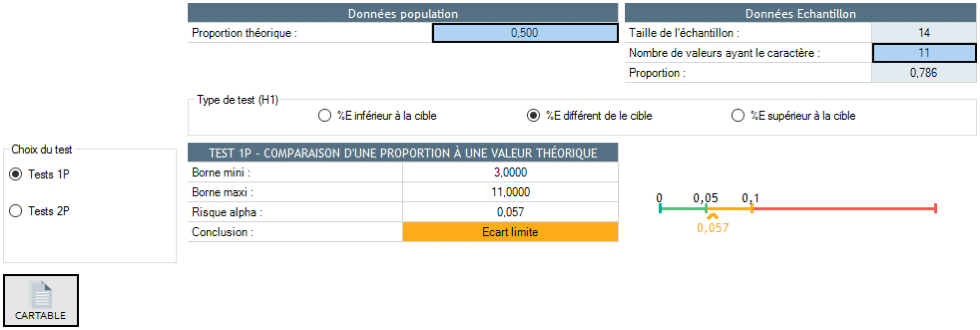
On observe que cet écart est limite.
Comme pour l’exemple précédent, les tests non paramétriques n’ont pas besoin de supposer un type de distribution particulière pour calculer le risque alpha du test. Ils sont très élégants et se basent sur des propriétés numériques. De plus, ils sont très peu sensibles aux valeurs aberrantes et sont donc conseillés dans ce cas.