Um den zentralen Grenzwertsatz zu erklären, nehmen wir Folgendes als Ausgangspunkt. Gott würfelt nicht, sagte einmal A.Einstein über die Quantenmechanik und stellte damit eine der Grundlagen der modernen Physik in Frage. Die Experimente des 20. Jahrhunderts haben ihn jedoch Lügen gestraft und es ist mittlerweile anerkannt, dass alle Observablen in dieser Welt nach Verteilungswahrscheinlichkeiten regieren und der Heisenbergschen Unschärferelation unterliegen. Die Welt ist zufällig
Das Verständnis von Zufallsphänomenen ist grundlegend, um zu verstehen, wie die Welt funktioniert. Nun kann man ein zentrales Theorem der statistischen Datenanalyse mathematisch beweisen: das zentrale Grenztheorem.
Jedes System, das sich aus der Summe vieler voneinander unabhängiger Faktoren gleicher Größenordnung ergibt, erzeugt eine Verteilungsregel, die zu einer Normalverteilung tendiert.
Dieses Theorem zeigt die Bedeutung der Normalverteilung bei der Analyse der Variabilität einer Observable. Um es zu veranschaulichen, werfen wir einen Würfel 1000 Mal hintereinander und beobachten die Verteilung der Ergebnisse :

Die Verteilung folgt einer Gleichverteilung, d. h. die Wahrscheinlichkeit, dass der Würfel auf 1, 2, 3, 4, 5 oder 6 fällt, ist gleich groß. Das Verteilungsgesetz ähnelt nicht der Normalverteilung.
Lassen Sie uns diesmal 10 Würfel 1000 Mal hintereinander werfen und beobachten, wie sich die Ergebnisse der Summe dieser 10 Würfel verteilen:
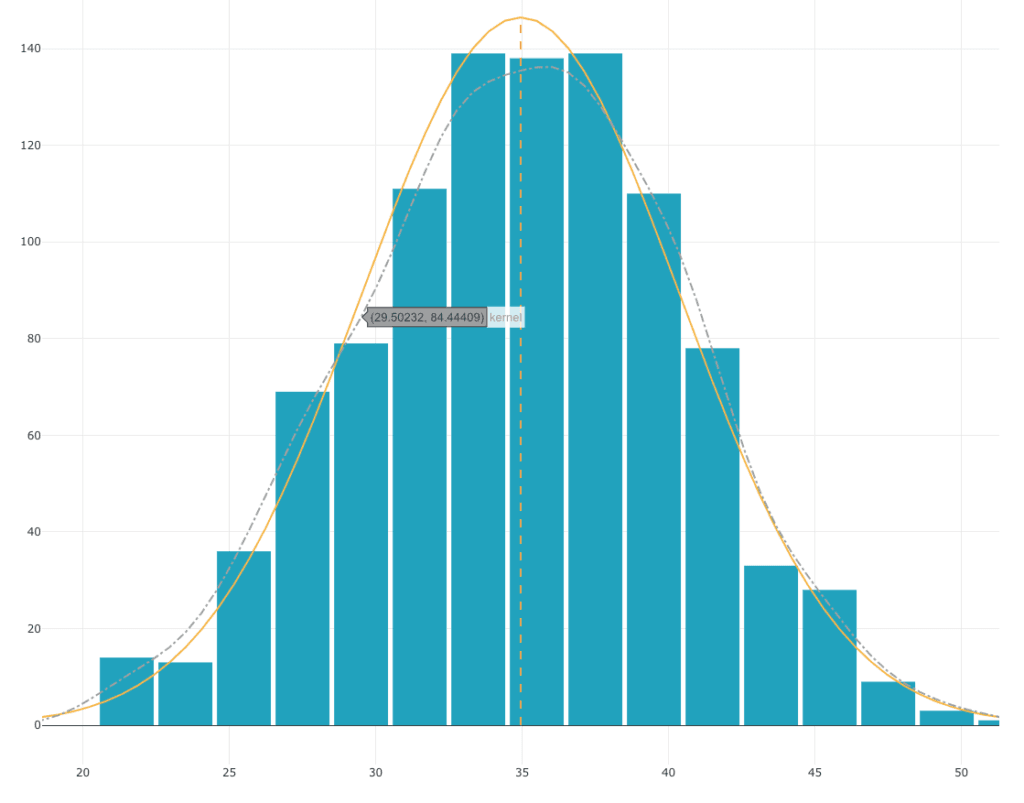
Obwohl jeder der Würfel einem Gleichverteilungsgesetz folgt, folgt die Verteilung der Summe der zehn Würfel einer Glockenkurve. Diese Verteilung ist einer Normalverteilung sehr ähnlich.
Wenn wir nämlich dem folgen, was der zentrale Grenzwertsatz :
- Wir haben ein System
- Ergibt sich aus der Summe vieler Faktoren (hier die Summe von 10 Würfeln).
- Unabhängig voneinander (das Ergebnis eines Würfels hat keinen Einfluss auf das Ergebnis eines anderen Würfels)
- Die Größenordnung der einzelnen Würfel ist gleichwertig
Die von diesem System erzeugte Verteilung tendiert tatsächlich zu einer Normalverteilung. Dies ist alles in allem recht intuitiv. Wenn man 10 Würfel wirft, gibt es nur eine einzige Kombination, die das Ergebnis 10 ergibt (alle Würfel sind auf 1 gefallen), während es Tausende von Kombinationen gibt, die das Ergebnis 35 ergeben. Folglich ist die Wahrscheinlichkeit, dass Ergebnisse nahe 35 auftreten, viel größer als die Wahrscheinlichkeit, dass extreme Ergebnisse wie 10 oder 60 auftreten. Die resultierende Verteilungsregel entspricht daher in etwa einer Normalverteilung.
Dies ist im Allgemeinen der Fall. Die Systeme, die wir normalerweise beobachten, weisen diese Art der Verteilung auf, da sie die Annahmen des zentralen Grenzwertsatzes erfüllen. Nehmen wir als Beispiel die Bearbeitung eines Werkstücks :
- Es handelt sich um ein System, das ein Merkmal hervorbringt.
- Die Abweichung des Merkmals vom Ziel ergibt sich aus der Summe vieler Faktoren (Vibrationen, Härte des Materials, Fehler bei der Positionierung des Werkzeugs usw....).
- Die Faktoren sind unabhängig voneinander (die Vibrationen der Maschine haben keinen Einfluss auf die Härte des Materials)
- Die Größenordnung dieser Abweichungen ist äquivalent
Die Verteilung der Münzen tendiert also zu einer Normalverteilung. Das ist das, was man beobachtet, wenn man eine Reihe von Münzen misst.
