Parametrikus és nem parametrikus statisztikai tesztek

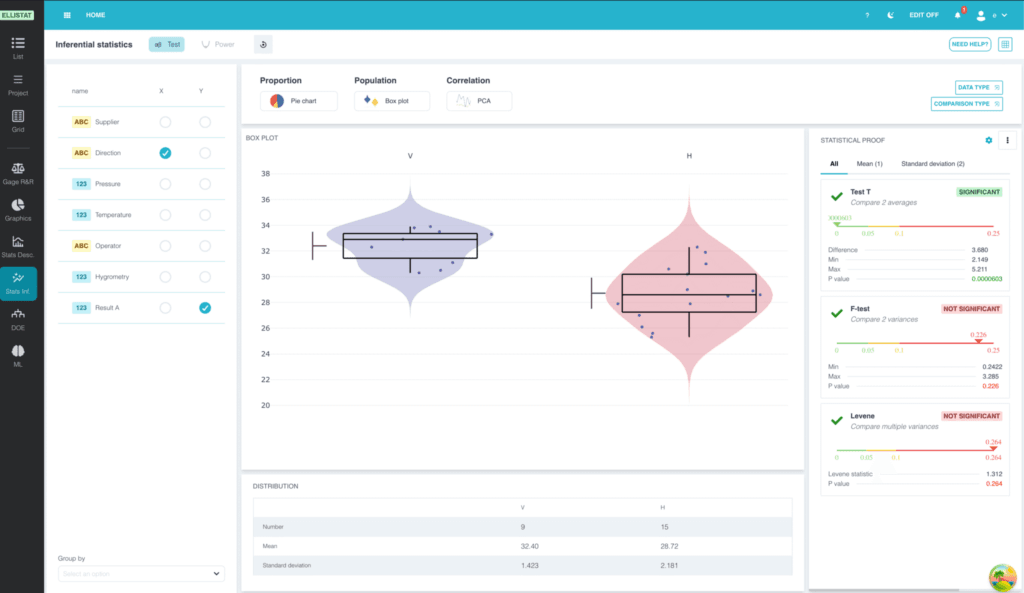
Mielőtt a parametrikus és nem parametrikus tesztek részleteibe bocsátkoznánk, nézzük meg, hogyan működik egy statisztikai teszt. A Ellistat adatelemző modul lehetővé teszi, hogy elvégezze ezeket a teszteket.

A statisztikai teszt a következőképpen működik:

• Olyan nullhipotézist veszünk figyelembe, amelyben nincs különbség a minták között.
• Kiszámítjuk annak a valószínűségét, hogy a nullhipotézis alapján megfigyelt mintákkal azonos konfigurációba esnek. Ezt a valószínűséget "alfa-kockázatnak" vagy "p-értéknek" nevezik.
• Ha az alfa-kockázat < 5%, akkor túl valószínűtlennek tekintjük, hogy a nullhipotézis alapján ilyen konfiguráció jöjjön létre. Ezért elutasítjuk a nullhipotézist, és úgy tekintjük, hogy a minták közötti különbség szignifikáns. Emiatt az Ellistat által javasolt statisztikai tesztek minden eredményéhez a következő skála szerinti alfa-kockázati értéket társítjuk:

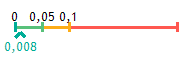
A skála alatti szám a teszt alfa-kockázatával egyenlő:

1. Ha az alfa kockázat < 0,01, a különbség nagyon szignifikánsnak tekintendő<.
2. Ha az alfa-kockázat < 0,05, a különbség szignifikánsnak tekinthető.
3. Ha az alfa-kockázat kisebb, mint 0,1, a különbség határesetnek tekinthető (nem mondható, hogy szignifikáns különbség van, de a hipotézis érdekes).
4. Ha az alfa-kockázat > 0,1, a különbséget jelentéktelennek tekintjük.

Példa

A statisztikai tesztek működésének szemléltetésére vegyük a következő példát.

Tegyük fel, hogy egy érme fej vagy írás feldobásával akarjuk megállapítani, hogy az érme fel van-e dobva. Feltételezzük, hogy az érme mindig írás lesz.

Throw n°1

Az első dobás után az érme írás lesz. Következtethetünk ebből arra, hogy az érme fel lett dobva?

Ránézésre elég kockázatos lenne arra fogadni, hogy az érme csőbe van húzva, mivel ugyanúgy megtörténhetett volna egy hagyományos érmével is.

Ebben az esetben a nullhipotézis a következő: az érme nincs feldöntve, tehát egy a kettőhöz az esélye, hogy fej vagy írás lesz. Annak valószínűsége, hogy a nem feldobott érme fejre jön, 50%.

Ennek eredményeképpen a fel nem dobott érme első feldobása után az írás valószínűsége 50%, azt mondjuk, hogy a teszt alfa kockázata:Alfa kockázat = 50%

Más szóval, 50% esély van arra, hogy a nullhipotézist követve ugyanarra az eredményre jutunk.

Throw n°2

A második dobás után az érme ismét írás lesz. Az alfa-kockázat a következő lesz:Alfa-kockázat = 25%

Ez azt jelenti, hogy a játékot megbundázták?

Felmerül tehát a kérdés: milyen alfa-kockázatnál mondhatjuk, hogy az érme felborult?

Általános szabályként az iparban az alfa-kockázati határértéket 5%-ben állapítják meg.

Más szóval :

• Ha az alfa-kockázat kisebb, mint 5%, a nullhipotézist elutasítjuk, és az érmét tippeltnek tekintjük.
• Ha az alfa-kockázat > 5%, akkor nem mondható, hogy az érme billen. Ez azonban nem jelenti azt, hogy az érme nincs feldobva, mivel ez a dobások számától függ.

Példa folytatása

Folytassuk a példánkat:

-3^th Dobás: az érme írás: alfa kockázat = 12,5%

-4^th Dobás: az érme írás: alfa kockázat = 6,75%

-5^th Dobás: az érme írás: alfa kockázat = 3,375%

Ebben az esetben 5^th Ezért azt mondhatjuk, hogy az érme 5%-nél kisebb kockázattal billen.

Parametrikus vs. nem-parametrikus tesztek

A populáció összehasonlításakor vagy egy populáció és egy elméleti érték összehasonlításakor két fő teszttípus létezik: a parametrikus tesztek és a nem parametrikus tesztek.

Parametrikus tesztek

A parametrikus tesztek azon a feltételezésen alapulnak, hogy a rendelkezésünkre álló adatok egy ismert típusú eloszlási törvényt követnek (általában a normális törvényt).

A statisztikai teszt alfa-kockázatának kiszámításához egyszerűen számítsa ki a minta átlagát és szórását, hogy hozzáférjen a minta eloszlási törvényéhez.

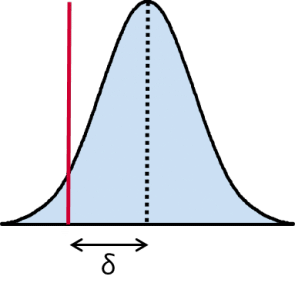
Az eloszlási törvény tökéletes ismeretében az alfa-kockázat a Gauss-eloszlásra vonatkozó elméleti számítások alapján kiszámítható.

Ezek a tesztek általában nagyon jók, de megkövetelik, hogy az adatok valóban kövessék a feltételezett eloszlást. Különösen érzékenyek a kiugró értékekre, és nem ajánlottak, ha kiugró értékeket észlelnek.

Nem parametrikus tesztek

A nem parametrikus tesztek nem tesznek feltevéseket az adatok eloszlásának típusára vonatkozóan. Kizárólag a minták numerikus tulajdonságain alapulnak. Íme egy példa egy nem parametrikus tesztre:

Ellenőrizni szeretnénk, hogy egy populáció mediánja eltér-e egy elméleti értéktől. Megmérünk 14 darabot, és a következő mintát kapjuk:

11-szer ugyanazon az oldalon a 14-ből

14-ből 11-szer az eredmény az elméleti medián alatt van. Ha a populáció mediánja megegyezik az elméleti értékkel, akkor 50% érmének kellene a medián felett és 50% érmének az alatt lennie. Annak megállapításához, hogy a medián eltérése az elméleti mediántól szignifikáns-e, csak azt kell ellenőriznünk, hogy a 14-ből 11-szeres gyakoriság szignifikánsan eltér-e az 50%-től.

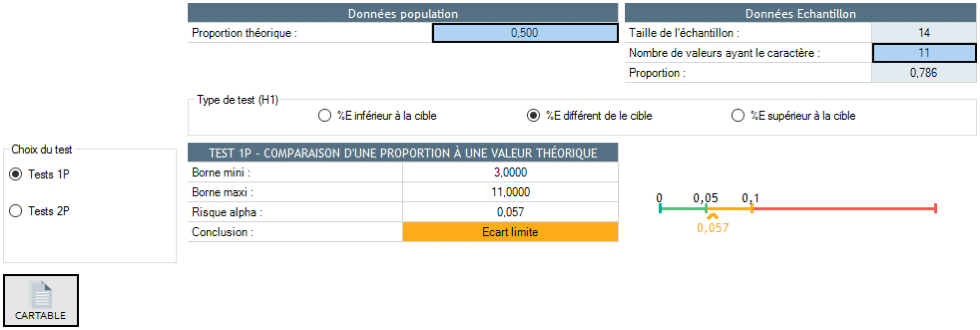
Ez a különbség határeset.

Az előző példához hasonlóan a nem-parametrikus tesztek esetében sem kell egy adott típusú eloszlást feltételezni a teszt alfa-kockázatának kiszámításához. Nagyon elegánsak, és numerikus tulajdonságokon alapulnak. Ráadásul nem túl érzékenyek a kiugró értékekre, ezért ebben az esetben ajánlott.