Le plan d’expérience de Taguchi est une méthode statistique utilisée pour améliorer la qualité des produits et des processus de fabrication. Développé par le Dr. Genichi Taguchi , ce plan vise à identifier les facteurs les plus influents sur la variation d’un produit ou d’un processus tout en minimisant le nombre d’expériences nécessaires.
Cette méthode organise les expériences de manière systématique et efficace, permettant d’analyser les effets de plusieurs variables simultanément. L’objectif principal est de rendre le produit ou le processus robuste contre les variations externes et internes, assurant ainsi une performance stable et de haute qualité.
Construire un plan d’expérience – Méthode Taguchi
Définir les facteurs et les niveaux
La définition des facteurs consiste choisir les facteurs à étudier. Pour choisir les bons facteurs nous vous conseillons tout d’abord de bien comprendre le process ou le produit concerné, puis de réaliser les étapes suivantes:
- Organiser des sessions de brainstorming avec une équipe multidisciplinaire pour générer une liste exhaustive de facteurs potentiels.
- Évaluer l’importance de chaque facteur en termes d’impact potentiel sur le résultat final. Prioriser les facteurs qui sont susceptibles d’avoir un effet significatif.
- Sélectionner les facteurs pertinents pour le plan d’expérience en fonction de l’importance du facteur, de votre capacité de le contrôler, de la facilité de le mesurer de manière fiable.
Pour chaque facteur identifié il faut ensuite définir les niveaux étudiés. Il est important de choisir des niveaux pertinents:
- Largeur de la plage : Sélectionner des niveaux qui couvrent une plage suffisamment large pour détecter les effets des facteurs, mais sans aller à des extrêmes irréalistes qui pourraient être inutiles ou dangereux.
- Praticabilité : Assurer que les niveaux choisis sont réalisables dans un contexte de production réelle.
Choix de la table
Une fois les facteurs identifiés, il vous faut créer le plan d’expérience, pour cela nous vous conseillons d’utiliser le module Data Analysis d’Ellistat qui dispose d’un moteur de création de plans d’expériences exclusif. Il est capable de trouver un plan avec la meilleure stratégie possible compte tenu d’une structuration d’interactions données. Les tables programmées dans Ellistat sont les tables L4, L8, L12, L16, L20 et L32.
Voici les éléments à bien prendre en compte pour la création de votre plan d’expérience selon la méthodologie de Taguchi :
Notion d’intéraction
On appelle interaction A*B le fait que le niveau de A ait une influence sur l’effet de B et réciproquement.
Exemple :
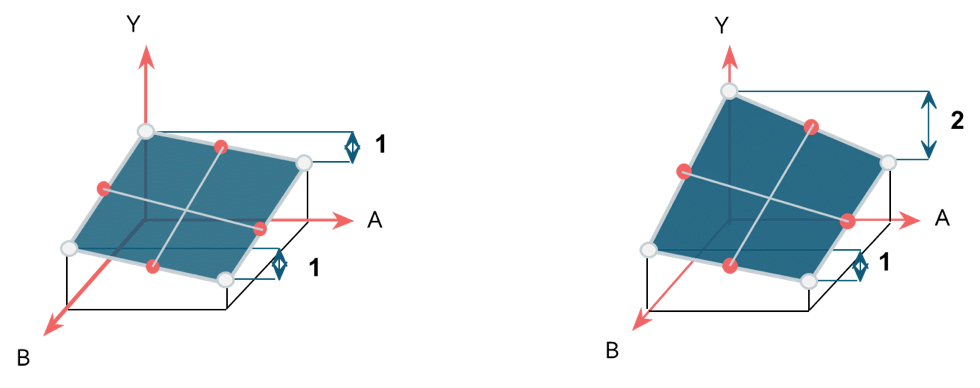
Sur l’exemple précédent on observe sur la figure de gauche :
Quel que soit le niveau du facteur B, l’effet de A sur le Y est le même et A a un effet de 1 sur la réponse. Il n’y a donc pas d’interaction entre A et B.
On observe sur la figure de droite :
Lorsque le niveau du facteur B est au minimum, l’effet de A sur le Y est de 2. Lorsque le niveau du facteur B est au maximum, l’effet de A sur le Y est de 1. L’effet de A varie en fonction du niveau de B et Il y a donc une interaction entre A et B.
Lorsqu’il y a une interaction, on modélise l’effet de l’interaction par un terme multiplicatif dans l’équation de prévision du Y, ici A*B.
La forme de l’équation de prévision serait :
Y=\alpha_0+\alpha_1*A+\alpha_2*B+\alpha_3*A*B
Le terme α3 correspond à l’interaction A*B
Notion d’alias
On appelle alias entre deux facteurs le fait que les facteurs aient le même niveau pour l’ensemble des expériences du plan d’expérience.
Par exemple supposons que l’on ait réalisé le plan d’expérience suivant :
| A | B | Y |
|---|---|---|
| 1 | 1 | 5 |
| 1 | 1 | 5 |
| 2 | 2 | 10 |
| 2 | 2 | 10 |
Les facteurs A et B varient en même temps, il n’est donc pas possible de différencier le facteur A du facteur B ni de dire lequel des deux provoque la variation du Y de 5 à 10 lorsqu’il passe de 1 à 2. On dira que ces deux facteurs sont alias.
Evidemment, lorsque l’on construit un plan d’expérience, on choisit soigneusement ses essais de manière à ce qu’aucun facteur ne soit alias d’un autre facteur. Toutefois, il est possible qu’un facteur soit alias avec une interaction. Prenons l’exemple suivant :
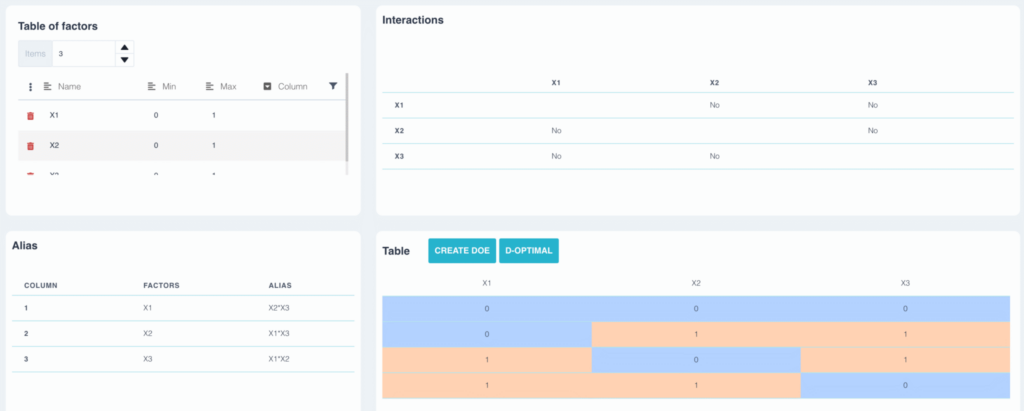
Dans cet exemple, nous avons construit un plan à trois facteurs en utilisant la table L4. On observe dans le tableau des alias :
- Le facteur a est alias avec l’interaction b*c
- Le facteur b est alias avec l’interaction a*c
- Le facteur c est alias avec l’interaction a*b
De la même manière que si deux facteurs sont alias, il ne sera pas possible de dire à la fin du plan d’expérience si l’effet constaté est dû au facteur a, à l’interaction bc ou à la somme des deux. On supposera donc que l’interaction bc est nulle, mais cela restera à vérifier expérimentalement.
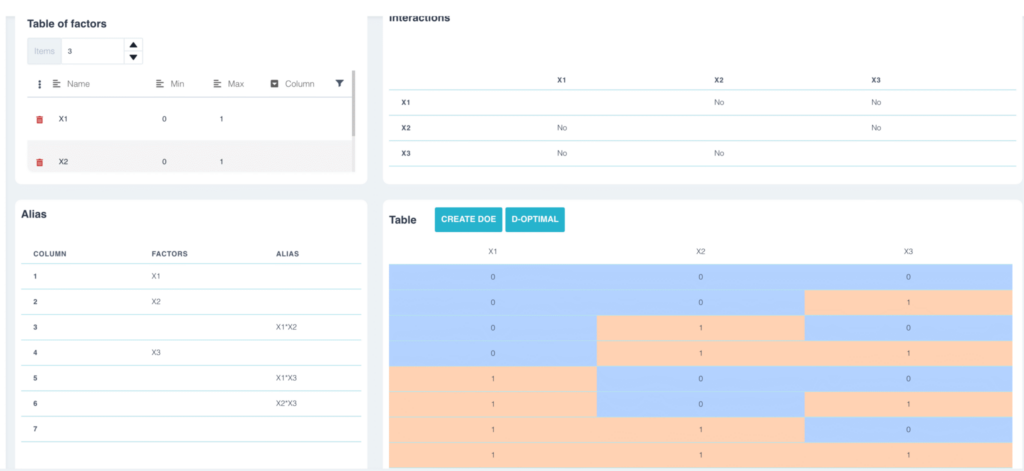
Pour éviter ce type de problématique, on choisit en général des plans d’expérience dans lequel aucun facteur n’est alias avec une interaction. Dans l’exemple précédent nous aurions pu choisir un plan L8 dont aucun des facteurs n’est alias avec une interaction.
Résolution d’un plan d’expérience
La résolution d’un plan d’expérience correspond au niveau d’alias de ce plan.
Résolution III
Un plan d’expérience est de résolution III si au moins un facteur (ordre I) est alias avec une interaction de type A*B (ordre II)
Ce type de plan permet de limiter fortement le nombre d’essais mais il fait l’hypothèse que l’ensemble des interactions est nul. Il faut faire attention dans l’interprétation des résultats et valider par des essais complémentaires l’hypothèse d’interactions nulles.
Exemple :
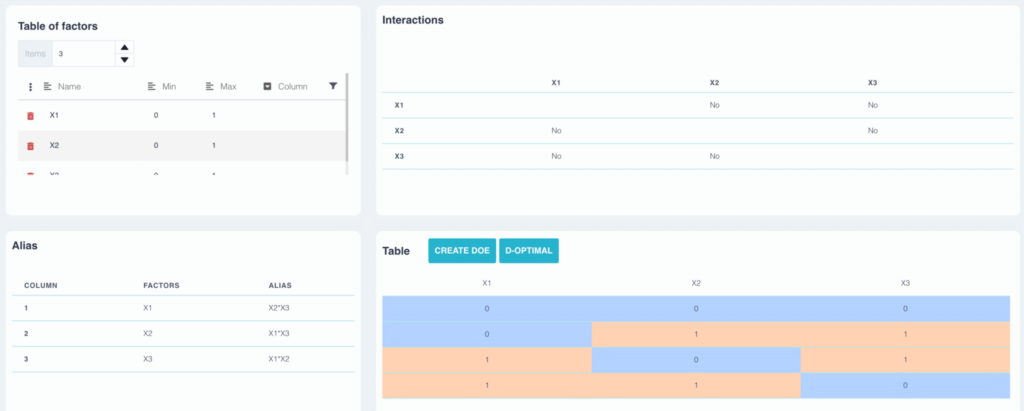
Dans le plan précédent le facteur a est alias avec l’interaction b*c. Le plan est de résolution III
Résolution IV
Un plan d’expérience est de résolution IV si :
- Aucun facteur n’est alias avec une interaction (ordre II)
- Au moins une interaction (ordre II) est alias avec une autre interaction (ordre II)
Ce type de plan permet de limiter le nombre d’essais. Il fait l’hypothèse que la majorité des interactions sont nulles sauf quelques-unes que l’on pourra identifier. Ce qui est en général le cas.
Les facteurs n’étant pas alias avec d’autres interactions, on pourra calculer sans ambiguïté l’effet de l’ensemble des facteurs.
C’est le type de plan que l’on utilise le plus souvent.
Exemple :
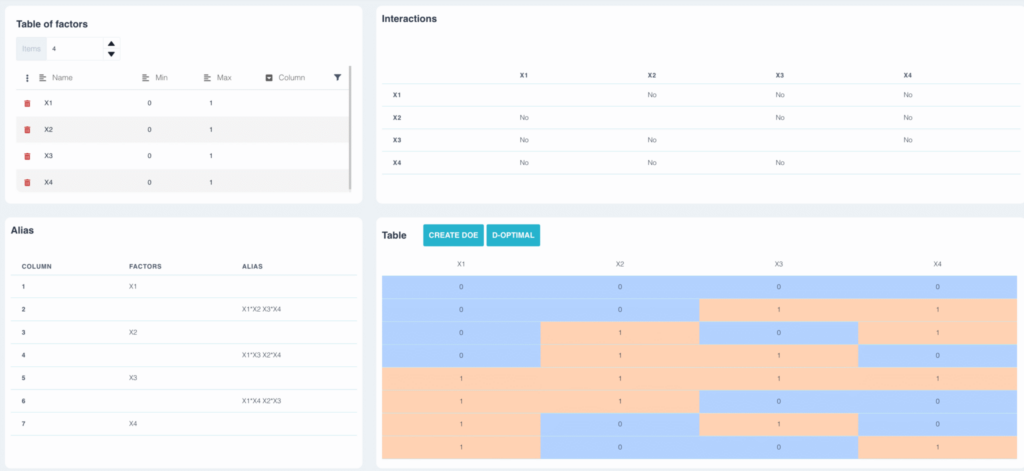
Dans le plan précédent aucun des facteurs n’est alias avec une autre interaction. Les interactions ab et cd sont alias, le plan est donc de résolution IV.
Résolution V
Un plan d’expérience est de résolution IV si :
- Aucun facteur n’est alias avec une interaction (ordre II)
- Aucune interaction (ordre II) n’est alias avec une autre interaction (ordre II) Ce type de plan permet de limiter le nombre d’essais par rapport au plan complet.
Les facteurs n’étant pas alias avec d’autres interactions, on pourra calculer sans ambiguïté l’effet de l’ensemble des facteurs.
Les interactions n’étant pas alias avec d’autres interactions, on pourra calculer sans ambiguïté l’effet de l’ensemble des interactions.
C’est le type de plan idéal, malheureusement il n’en existe qu’un seul à moins de 20 essais. Il s’agit d’un plan à 5 facteurs utilisant la table L16.


