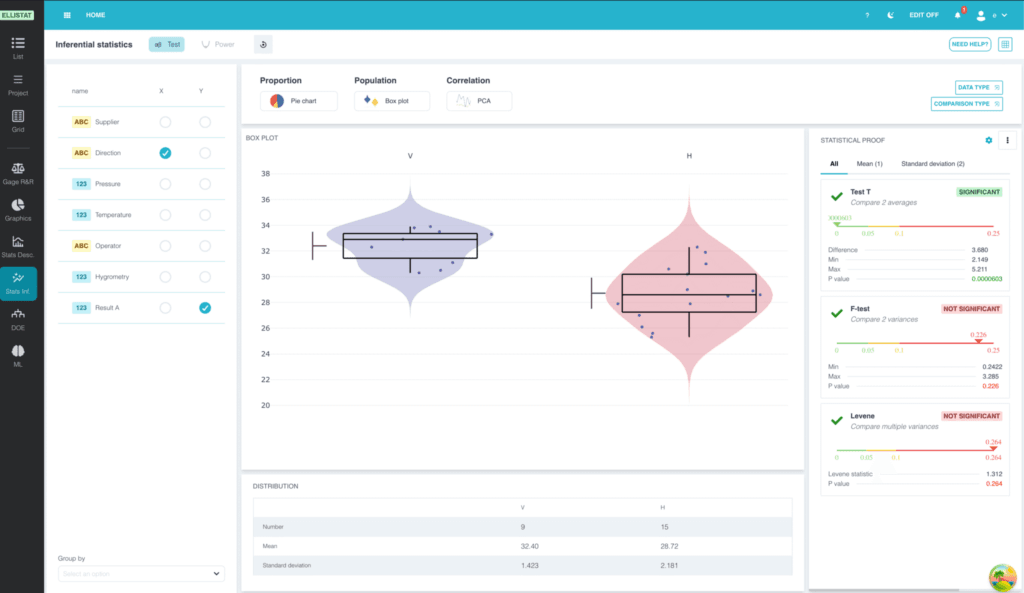
Bevor wir auf die parametrischen und nichtparametrischen Tests eingehen, wollen wir uns noch einmal vergegenwärtigen, wie ein statistischer Test funktioniert. Der Ellistat Data Analysis-Modul ermöglicht es Ihnen, diese Tests durchzuführen.
Ein statistischer Test funktioniert folgendermaßen:
- Es wird eine Nullhypothese betrachtet, bei der es keine Unterschiede zwischen den Stichproben gibt.
- Man berechnet die Wahrscheinlichkeit, in das gleiche Muster zu fallen, das man mit den beobachteten Stichproben bei Befolgung der Nullhypothese erhält. Diese Wahrscheinlichkeit wird als "Alpha-Risiko" oder "p-Wert" bezeichnet.
- Wenn das Alpha-Risiko < 5% ist, wird angenommen, dass es zu unwahrscheinlich ist, eine solche Konfiguration im Rahmen der Nullhypothese zu erhalten. Daher wird die Nullhypothese verworfen und der Unterschied zwischen den Stichproben als signifikant angesehen. Aus diesem Grund wird allen Ergebnissen der von Ellistat angebotenen statistischen Tests ein Wert für das Alpha-Risiko mit folgender Skala zugeordnet:
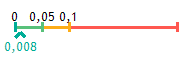
Die Zahl unterhalb der Skala entspricht dem Alpha-Risiko des Tests :
- Wenn das Alpha-Risiko < 0,01 ist, wird der Unterschied als hoch signifikant angesehen<.
- Wenn Alpha-Risiko < 0.05, wird der Unterschied als signifikant angesehen
- Wenn das Alpha-Risiko < 0,1 ist, wird der Unterschied als grenzwertig angesehen. (Man kann nicht sagen, dass es einen signifikanten Unterschied gibt, aber die Hypothese ist interessant).
- Wenn das Alpha-Risiko > 0,1 ist, wird der Unterschied als nicht signifikant betrachtet.
Beispiel
Um die Funktionsweise eines statistischen Tests zu veranschaulichen, nehmen wir das folgende Beispiel.
Angenommen, wir möchten erkennen, dass eine Münze pipettiert wird, und werfen eine Münze. Wir gehen davon aus, dass die Münze immer auf Kopf fällt.
Wurf Nr. 1
Nach dem ersten Wurf fällt die Münze auf Zahl. Kann man daraus schließen, dass die Münze gepipet ist?
Auf den ersten Blick wäre es ziemlich gewagt, darauf zu wetten, dass die Münze pipettiert wird, denn das hätte genauso gut mit einer Standardmünze passieren können.
In diesem Fall lautet die Nullhypothese: Die Münze ist nicht gepipet, also hat sie eine Chance von 1:2, auf Kopf oder Zahl zu fallen. Die Wahrscheinlichkeit, dass eine nicht gepipte Münze auf Kopf fällt, beträgt 50%.
Die Wahrscheinlichkeit, nach dem ersten Wurf einer nicht gepipten Münze Kopf zu erhalten, beträgt 50%, das Alpha-Risiko des Tests ist also:Alpha-Risiko = 50%
D. h., es besteht eine 50%-Chance, das gleiche Ergebnis zu erhalten, wenn man der Nullhypothese folgt.
Wurf Nr. 2
Nach dem zweiten Wurf fällt die Münze wieder auf Kopf. Das Alpha-Risiko wird:Alpha-Risiko = 25%
Kann man daraus schließen, dass die Münze gepipet ist?
Es stellt sich also die Frage: Ab welchem Alpha-Risiko kann man sagen, dass die Münze gepipet ist?
In der Regel wird in der Industrie das Alpha-Grenzrisiko bei 5% gewählt.
D. h. :
- Wenn das Alpha-Risiko < 5% ist, wird die Nullhypothese verworfen und die Münze als gepipettiert betrachtet.
- Wenn das Alpha-Risiko > 5% ist, kann man nicht sagen, dass die Münze gepipet ist. Das bedeutet jedoch nicht, dass die Münze nicht gepipet ist, da dies von der Anzahl der Würfe abhängt, die man gemacht hat.
Fortsetzung des Beispiels
Führen wir unser Beispiel weiter aus:
-3ème Wurf, die Münze fällt auf Zahl: Alpha-Risiko = 12.5%
-4ème Wurf, die Münze fällt auf Zahl: Alpha-Risiko = 6.75%
-5ème Wurf, die Münze fällt auf Zahl: Alpha-Risiko = 3.375%
In diesem Fall wird ab dem 5.ème Wurf in Folge, bei dem die Münze auf Kopf fällt, kann man also sagen, dass die Münze mit einem Risiko von weniger als 5% pipettiert wird.
Parametrische vs. nicht-parametrische Tests
Wenn man Populationsvergleiche durchführt oder eine Population mit einem theoretischen Wert vergleicht, gibt es zwei große Testfamilien: parametrische Tests und nicht-parametrische Tests.
Parametrische Tests
Parametrische Tests funktionieren unter der Annahme, dass die Daten, die man zur Verfügung hat, einem bekannten Typ von Verteilungsgesetz folgen (in der Regel der Normalverteilung).
Um das Alpha-Risiko des statistischen Tests zu berechnen, müssen Sie nur den Mittelwert und die Standardabweichung der Stichprobe berechnen, um auf das Verteilungsgesetz der Stichprobe zuzugreifen.
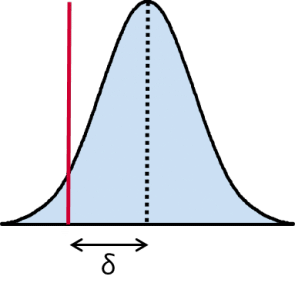
Da das Verteilungsgesetz somit vollkommen bekannt ist, kann man das Alpha-Risiko auf der Grundlage der theoretischen Berechnungen der Gaußschen Verteilung berechnen.
Diese Tests sind in der Regel sehr fein, setzen aber voraus, dass die Daten tatsächlich dem angenommenen Verteilungsgesetz folgen. Insbesondere sind sie sehr anfällig für Ausreißer und werden nicht empfohlen, wenn Ausreißer festgestellt werden.
Nicht-parametrische Tests
Nichtparametrische Tests machen keine Annahmen über die Art der Verteilungsgesetze der Daten. Sie stützen sich lediglich auf die numerischen Eigenschaften der Stichproben. Hier ein Beispiel für einen nichtparametrischen Test :
Man möchte überprüfen, ob sich der Median einer Population von einem theoretischen Wert unterscheidet. Wir messen 14 Stück und erhalten die folgende Stichprobe:

11 Mal auf derselben Seite von 14
In 11 von 14 Fällen liegt das Ergebnis unter dem theoretischen Median. Wenn der Median der Population dem theoretischen Wert entspricht, sollten 50% der Münzen über dem Median und 50% der Münzen unter dem Median liegen. Um über die Signifikanz der Abweichung des Medians vom theoretischen Median zu entscheiden, müssen wir also nur prüfen, ob sich die Häufigkeit von 11 von 14 Mal signifikant von 50% unterscheidet.
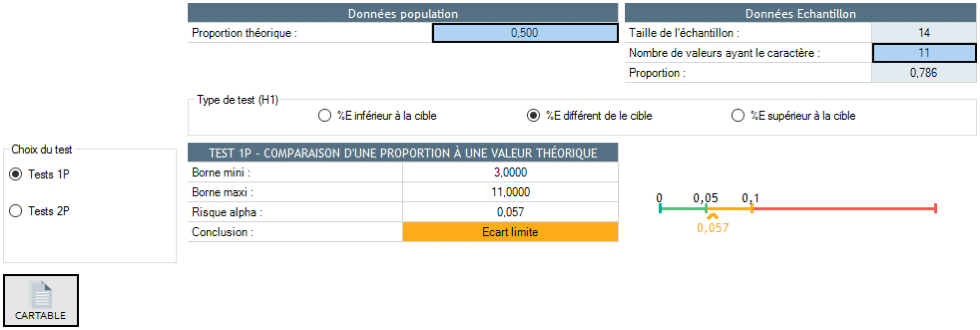
Wir stellen fest, dass diese Abweichung grenzwertig ist.
Wie im vorherigen Beispiel müssen nichtparametrische Tests keinen bestimmten Verteilungstyp voraussetzen, um das Alpha-Risiko des Tests zu berechnen. Sie sind sehr elegant und basieren auf numerischen Eigenschaften. Außerdem sind sie sehr unempfindlich gegenüber Ausreißern und werden daher in diesem Fall empfohlen.